Rotational Dynamics Notes | Class 12

Rigid body

A body is said to be rigid if its molecular separations are constant even when it is in translational or rotational motion.

Moment of force:

Moment of force is defined as the product of force acting on an object and its perpendicular distance from the axis of rotation. It is a type of static force. In physics, moment of force is a measure of its tendency to cause a body to rotate about a specific point or axis.

From figure,

Moment of force = F × OA

[Where the axis of rotation passes through O.]

Or, Moment of force = F × OB sin$\theta $ [$\because $ sin$\theta $ = $\frac{OA}{OB}$ $\therefore $ OA = OB sin$\theta $]

$\therefore $ Moment of force = F r sin$\theta $

Torque ($\tau $):

Torque is the turning effect of force. It is a movement type force. Torque is the measure of force that causes an object to rotate about an axis. Just like how force causes an object to accelerate in linear kinematics, torque is what causes an object to acquire angular acceleration. Mathematically, it can be defined as the product of force and its perpendicular distance from the axis of rotation. It is denoted $\tau $ by and given by

$\tau $ = F r sin$\theta $

In vector notation, above result can be expressed as

$\overrightarrow{\tau }$ = $\overrightarrow{r}$ × $\overrightarrow{F}$

Special Cases:

When $\theta $ = 0^o,

Torque, $\tau $ = F r sin0^o = 0 (Minimum)

When $\theta $ = 90^o,

Torque, $\tau $ = F r sin90^o = F.r (Maximum)

Parallel Forces:

Two forces are said to be parallel if their lines of action are parallel to each other.

Couple:

Two equal and unlike parallel forces acting on an object at different points is known as couple.

Moment of Inertia (I)

In linear motion mass of a body is the measure of inertia (i.e. the measure of difficulty to change of state of rest or uniform motion.) Similarly, in rotational motion the moment of inertia of a body is the measure of rotational inertia (i.e. the measure of difficulty to change the state of rest or uniform rotational motion.)

Mathematically, the moment of inertia of a rigid body about a particular axis is defined as the sum of products masses of all particles constituting the body and square of their perpendicular distance from the axis of rotation. It is denoted by ‘I’ and given by I = $\Sigma $mr². Its unit is Kgm² and the dimensional formula is [ML²T⁰].

The moment of inertia depends upon

(i) mass

(ii) Radius (perpendicular distance from axis of rotation)

(iii) distribution of mass.

Note-2: The moment of inertia of two bodies of same mass and radius may be different. For example: A ring and a disc of same mass and radius have different value of moment of inertia.

The moment of inertia of the ring is greater than that of the disc.

Comparison Rotational motion with linear motion

	Translational/Linear Motion	Rotational Motion
1.	Mass, m Unit: kg	Moment of inertia, I = $\Sigma $mr² Unit: kgm²
2.	Linear displacement, s or d Unit: m	Angular displacement, $\theta $ Unit: radian Also, 180^o = 200^g= $\pi $^c
3.	Linear velocity, v = $\frac{s}{t}$ , $\frac{ds}{dt}$ , $\frac{∆s}{∆t}$ Unit: ms^–1	Angular velocity, $\omega $ = $\frac{\theta }{t}$, $\frac{d\theta }{dt}$,$\frac{∆\theta }{∆t}$ Also, v = r $\omega $ Unit: rads^–1
4.	Linear momentum, P = mv Unit: kg m s⁻¹	Angular momentum, L = I $\omega $ Unit: kg m² s⁻¹ Also, L = r × P
5.	Linear acceleration, a = $\frac{dv}{dt}$, $\frac{∆v}{∆t}$, $\frac{v\,-u}{t}$, $\frac{{{\text{v}}_{\text{2}}}\text{-}{{\text{v}}_{\text{1}}}}{\text{t}}$ Unit: ms^–2	Angular velocity, $\alpha $ = $\frac{d\omega }{dt}$, $\frac{{{\omega }_{}}\,-\,{{\omega }_{1}}}{t}$, $\frac{{{\omega }_{2}}\,-\,{{\omega }_{1}}}{t}$ Unit: rad s^–2 Also, a = r $\alpha $
6.	(i) Force, F = ma Also, (ii) F = $\frac{dP}{dt}$ Unit: N	Torque, $\tau $ = I$\alpha $ Also, (ii) $\tau $ = $\frac{dL}{dt}$ (iii) $\tau $ = r × F Unit: Nm
7.	Principle of conservation of Linear momentum, For F_ext= 0, P = constant	Principle of conservation of Angular momentum, For ${{\tau }_{ext}}$ = 0, L = constant (= Iw) i.e. I₁${{\omega }_{1}}$ = I₂${{\omega }_{2}}$
8.	Linear K.E. = $\frac{1}{2}$m v² Unit: J	Rotational K.E. = $\frac{1}{2}$I${{\omega }^{2}}$ Unit: J
9.	Work done, W = F×S Unit: J	Work done, W = $\tau $ × $\theta $ Unit: J
10.	Power P = $\frac{W}{t}$ Also, P = FV Unit: Watt	Power P =$\frac{W}{t}$ Also, P = $\tau $ $\omega $ Unit: Watt
Equations Of Motion
11.	v = u+ a t	$\omega $ = ${{\omega }_{o}}$+ $\alpha $t
12.	v² = u²+ 2as	${{\omega }^{2}}$= ${{\omega }_{o}}^{2}$+ 2$\alpha $$\theta $
13.	s = ut + $\frac{1}{2}$at²	$\theta $ = ${{\omega }_{o}}$t + $\frac{1}{2}$$\alpha $t²

Radius of gyration (R):You will enjoy the numerical problems of rotational dynamics if you are able to compare the rotational motion with linear motion.

The radius of gyration of a rigid body rotation about a particular axis is defined as the perpendicular distance of its centre of mass from the axis of rotation.

Let us consider a rigid body consisting of a large number of particles of mass m₁, m₂, m₃, …… m_n at a distance of r₁, r₂, r₃, ……….. r_n from the axis of rotation. From the definition of moment of inertia, we can write

I = m₁r₁² + m₂r₂² + m₃r₃² + …… + mnrn²

For m₁ = m₂ = m₃ = …………. mⁿ = m.

I = mr₁² + mr₂² + mr₃² + …… mr_n² ………. (i)

Let C.M. be the centre of mass of the rigid body which is at a distance of R from the axis of rotation. This means ‘R’ is the radius of gyration of the given body. Let ‘M’ be the whole mass of the given body. Again, the moment of inertia can be written as

I = MR² ………. (ii)

From (i) and (ii)

MR² = m (r₁²+r₂²+r₃²)

Or, nmR² = m(r₁²+r₂²+r₃²+….. +rn²)

$\therefore $ R = $\sqrt{\frac{{{r}_{1}}^{2}+{{r}_{2}}^{2}+{{r}_{3}}^{2}+…….+{{r}_{n}}^{2}}{n}}$,

This is the required expression for the radius of gyration.

Moment of inertia of a uniform rod with axis of rotation passing through its centre and perpendicular to its length.

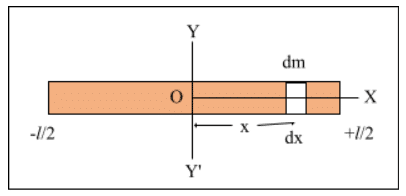
Let us consider a uniform rod of length ‘l‘ and mass ‘m’ let the axis of rotation of the rod YOY’ passes through its centre and is perpendicular to its length. Let ‘dm’ be the small mass of a small section ‘dx’ that is at a distance of ‘x’ from the axis of rotation.

Since mass of ‘l‘ length of rod = m

Mass of unit length of rod = m/l

and, mass of dx length of rod = $\frac{m}{l}$ dx = dm (say)

Now, the moment of inertia of elementary mass ‘dm’ is given as

dI = dm x²

Or, dI = $\frac{m}{l}$.dx.x²

Or, dI = $\frac{m}{l}$.x²dx ………. (i)

Total moment of inertia of the whole rod can be obtained by integrating (i) from x = –l/2 to x = l/2, i.e.

$\int\limits_{-l/2}^{l/2}{{}}$dI = $\int\limits_{-l/2}^{l/2}{{}}$$\frac{m}{l}$.x².dx

Or, I = $\frac{m}{l}$$\int\limits_{-l/2}^{l/2}{{}}$x²dx

Or, I = $\frac{m}{l}$$\left[ \frac{{{x}^{3}}}{3} \right]$$\underset{-l/2}{\overset{l/2}{\mathop{\underset{{}}{\overset{{}}{\mathop{{}}}}\,}}}\,$

Or, I = $\frac{m}{3l}$$\left[ {{\left( \frac{l}{2} \right)}^{3}}-{{\left( \frac{-l}{2} \right)}^{3}} \right]$

Or, I = $\frac{m}{3l}$$\left[ \frac{{{l}^{3}}+{{l}^{3}}}{8} \right]$

Or, I = $\frac{m}{3l}$. $\frac{2{{l}^{3}}}{8}$

$\therefore $ I = $\frac{\mathbf{m}{{l}^{\mathbf{2}}}}{\mathbf{12}}$

This is the required expression for moment of inertia of uniform rod with axis of rotation passing through its centre and perpendicular to the length.

Note

The moment of inertia of a uniform rod with its axis passing through one of its ends and perpendicular to its length is given by

I = $\frac{\mathbf{1}}{\mathbf{3}}\mathbf{m}{{l}^{\mathbf{2}}}$ [ Hint: Take limit: 0 to l ]

Moment of inertia of a uniform rod with axis of rotation passing through one of its ends and perpendicular to its length.

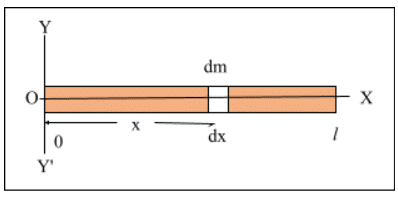
Let us consider a uniform rod of length ‘l‘ and mass ‘m’ let the axis of rotation of the rod YOY’ passes through one of its ends and is perpendicular to its length. Let ‘dm’ be the small mass of a small section ‘dx’ which is at a distance of ‘x’ from the axis of rotation.

Since mass of ‘l‘ length of rod = m

Mass of unit (1) length of rod = $\frac{m}{l}$

and, mass of dx length of rod = $\frac{m}{l}$ dx = dm (say)

Now, the moment of inertia of elementary mass ‘dm’ is given as

dI = dm x²

Or, dI = $\frac{m}{l}$.dx.x²

Or, dI = $\frac{m}{l}$.x²dx ………. (i)

Total moment of inertia of the whole rod can be obtained by integrating (i) from x = 0 to x = l, i.e.

$\int\limits_{0}^{l}{{}}$dI = $\int\limits_{0}^{l}{{}}$$\frac{m}{l}$.x².dx

Or, I = $\frac{m}{l}$$\int\limits_{0}^{l}{{}}$x²dx

Or, I = $\frac{m}{l}$$\left[ \frac{{{x}^{3}}}{3} \right]$$\underset{0}{\overset{l}{\mathop{\underset{{}}{\overset{{}}{\mathop{{}}}}\,}}}\,$

Or, I = $\frac{m}{l}$$\left[ {{\left( \frac{{{l}^{3}}}{3} \right)}^{{}}}-\left( \frac{{{0}^{3}}}{3} \right) \right]$

Or, I = $\frac{m}{l}$$\left[ \frac{{{l}^{3}}}{3} \right]$

Or, I = $\frac{m{{l}^{2}}}{3}$

$\therefore $ I = $\frac{\mathbf{1}}{\mathbf{3}}\mathbf{m}{{l}^{\mathbf{2}}}$

This is the required expression for moment of inertia of uniform rod with axis of rotation passing through one of its ends and perpendicular to the length.

Rotational kinetic Energy of a Rigid Body:

Let us consider a rigid body consisting of a large number of particles of mass m₁, m₂, m₃, …….. m_n at a distance of r₁, r₂, r₃, …… r_n respectively from the axis of rotation. Let the body rotate with constant angular velocity ‘$\omega $’ about the given axis as shown in figure above.

Kinetic energy of particle- m₁ = $\frac{1}{2}$m₁v₁²

K.E. of particle- m₁ = $\frac{1}{2}$m₁ $\omega $₁² r₁² [$\because $ v = $\omega $r]

Similarly, K.E. of particle- m₂ = $\frac{1}{2}$m₂$\omega $₂²r₂²

K.E. of particle- m_n = $\frac{1}{2}$m_n $\omega $_n²r_n²

Now, total kinetic energy of rotating body can be written as

Rotational kinetic energy = $\frac{1}{2}$m₁$\omega $₁² r₁² + $\frac{1}{2}$m₂$\omega $₂²r₂²+ $\frac{1}{2}$m₃$\omega $₃²r₃² + ….. $\frac{1}{2}$m_n$\omega $_n²r_n²

For a given rigid body, the angular velocities of all particles are the same. i.e.

$\omega $₁ = $\omega $₂ = $\omega $₃ = …………… $\omega $_n = $\omega $ (say)

Then above equation becomes,

Rotational K.E = $\frac{1}{2}$m₁$\omega $²r₁² + $\frac{1}{2}$m₂$\omega $²r₂²+ $\frac{1}{2}$m₃$\omega $²r₃²….$\frac{1}{2}$m_n$\omega $²r_n²

Or, rotational K.E. = $\frac{1}{2}$ (m₁r₁²+m₂r₂²+ …. +m_nr_n²) × $\omega $²

Or, rotational K.E. = $\frac{1}{2}$($\Sigma $mr²) $\omega $²

Or, rotational K.E. = $\frac{1}{2}$ I × $\omega $² [$\because $I = $\Sigma $mr²]

$\therefore $ Rotational K.E. = $\frac{\mathbf{1}}{\mathbf{2}}$I $\omega $²

This is the required expression for rotational kinetic energy of a rotating rigid body.

Relation between torque ($\tau $) and momentum of inertia.

The torque of a rigid body rotating about a particular axis is defined as the product to force applied and the perpendicular distance of the object from the axis of rotation. It is denoted by ‘$\tau $’ and given as $\tau $ = F× r

It is the turning effect of force on an object it can also be defined as the rate of change of angular momentum, i.e. $\tau $ = $\frac{dL}{dt}$, Where L is angular momentum.

Let us consider a rigid body consisting of a large number of particles of masses m₁, m₂, m₃… m_n at a distance of r₁, r₂, r₃, …… r_n respectively from the axis of rotation. Let the body rotate with constant angular velocity ‘$\omega $’ about the given axis as shown in figure above.

Acceleration of particle- m₁ = α₁r₁

[$\because $ V = $\omega $r ⇒ $\frac{dv}{dt}$ = $\frac{d\,(\omega \,r)}{dt}$ ⇒ a = $\alpha $.r]

Then, force on particle m₁ = m₁ $\alpha $₁r₁ [$\because $ F = ma]

Or, torque on particle-m₁ = (m₁ $\alpha $₁r₁) × r₁ [$\because $ Torque, $\tau $ = F ×r]

Torque on particle-m₁ = m₁ $\alpha $₁r₁²

Similarly,

Torque on particle-m₂ = m₂ $\alpha $₂r₂²

Torque on particle-m₃ = m₃ $\alpha $₃r₃²

Torque on particle-m_n = m_n $\alpha $_nr_n²

Now the total torque on the rigid body can be expressed as

$\tau $ = m₁ $\alpha $₁r₁²+ m₂ $\alpha $₂r₂²+ m₃ $\alpha $₃r₃² + ……. m_n $\alpha $_nr_n²

For a given rigid body, the angular velocity of all particles are the same and hence the angular acceleration are also the same. i.e.

$\alpha $₁= $\alpha $₂= $\alpha $₃ = …. $\alpha $_n= $\alpha $ (say)

Then above equation becomes,

$\tau $ = (m₁r₁²+ m₂r₂²+ m₃r₃² + ……. m_nr_n²) $\alpha $

$\tau $ = $\Sigma $mr² × $\alpha $

Since, moment of inertia, I = $\Sigma $mr²

$\therefore $ Torque, $\tau $ = I $\alpha $

This is the required expression for torque in terms of moment of inertia.

Angular momentum (L) and its relation with moment of inertia:

The angular momentum of a rigid body rotating about a particular axis is defined as the product of linear momentum and perpendicular distance from the axis of rotation. It is denoted by ‘L’ and given by

$\overrightarrow{L}$= $\overrightarrow{r}$ × $\overrightarrow{P}$

Taking magnitude only, L = P × r

Let us consider a rigid body consisting of a large number of particles of masses m₁, m₂, m₃ …. m_n at a distance of r₁, r₂, r₃, ….. r_n respectively from the axis of rotation. Let the body rotate with angular velocity ‘$\omega $’ about the given axis as shown in figure above.

From the definition, angular momentum of particle m₁ is

L₁ = P₁r₁ = m₁v₁ × r₁

Or, L₁ = m₁× $\omega $₁r₁ × r₁

Or, L₁ = m_{1 $\omega $1}r₁²

Similarly,

angular momentum of particle- m₂, L₂ = m₂r₂²$\omega $₂

angular momentum of particle- m_3, L₃ = m₃r₃²$\omega $₃

angular momentum of particle- m_n, L_n = m_nr_n²$\omega $_n

Now, total angular momentum of the rigid body is

L = m₁r₁²$\omega $₁+ m₂r₂²$\omega $₂ + m₃r₃²$\omega $₃ + ….. m_nr_n²$\omega $_n

For a given rigid body, the angular velocity of all particles are the same. i.e.

$\omega $₁= $\omega $₂ = $\omega $₃ ……. $\omega $_n = $\omega $ (say)

L = (m₁r₁² + m₂r₂²+ m₃r₃² + …. m_nr_n²) $\omega $

= $\Sigma $mr²× $\omega $

Since, moment of inertia, I = $\Sigma $mr²

$\therefore $ L = I$\omega $

This is the required expression for angular momentum of a rigid body.

Principle of conservation of Angular Momentum:

Principle of conservation of Angular Momentum states “In the absence of external force, the total angular momentum of an isolated rotating object remains constant.” i.e.

L = I$\omega $ = constant

Let us consider a rigid body of moment of inertia (I) rotates about a particular axis with angular velocity ‘$\omega $’. From the definition of torque.

Torque ($\tau $) = $\frac{dL}{dt}$

In the absence of external torque, i.e. $\tau $ = 0

From above equation

$\frac{dL}{dt}$ = 0 [ $\because $$\tau $ = 0]

Or, L = constant [ Since the derivative of constant is zero]

Or, L = I$\omega $ = constant

Or, I₁$\omega $₁ = I₂$\omega $₂

$\therefore $ I₁$\omega $₁ = I₂$\omega $₂ = L = Constant

This is conservation of angular momentum.

Note

1. Since I$\omega $ = constant

I × $\frac{2\pi }{T}$= Constant [$\because $$\omega $ = $\frac{2\pi }{T}$]

$\therefore $ I ∝ T

2. Since I$\omega $ = constant

I × 2$\pi $f = constant [$\because $$\omega $ = 2$\pi $f]

$\therefore $ f ∝ $\frac{\mathbf{1}}{\mathbf{I}}$

Short Questions:

If the ice on the polar caps of the earth melts, how will it affect the duration of the day? Explain.
Can you distinguish a raw egg and a hard boiled egg by spinning each one on the table? Explain.
If earth shrinks, how will the duration of a day be affected?
The cap of a bottle can be easily opened with the help of two fingers rather than with one finger. Why?
A ballet dancer stretches her hands when she wants to come to rest. Why?
A fan with blades takes a longer time to come to rest than without blades. Why?
A ballet dancer can increase her arms to reduce her motion. Explain
A dancer girl is rotating over a turntable with her arms outstretched. If she lowers her arms, how does this affect her motion?
Explain why spokes are fitted in the cycle wheel.
What is the counterpart of the mass and force in rotational motion?
If meteorites strike the earth, the earth will slow down slightly. Why?

Couple, Moment of Couple and Expression for work done by Couple.

Couple:

Two equal and opposite forces (unlike force) acting on a body at two different points which rotate or tend to rotate the object is called couple.

Moment of couple:

Moment of couple can be defined as the product of one of its forces and perpendicular distance between them.

Moment of couple is denoted by ‘$\tau $’ and given by

$\tau $ = F×2r

Work done by couple:

Let us consider a couple (two equal and opposite forces) acting tangentially on a wheel at two opposite points A and B, which rotates the wheel through angle $\theta $.

Work done by the couple is

W = F × $\overset\frown{AA’}$ + F × $\overset\frown{BB’}$ ……… (i)

Since, $\theta $ = $\frac{l}{r}$= $\frac{\overset\frown{AA’}}{r}$= $\frac{\overset\frown{BB’}}{r}$

$\therefore $ $\overset\frown{AA’}$= $\theta $r and $\overset\frown{BB’}$ = $\theta $r

$\therefore $ W = F × $\theta $r + F × $\theta $r

$\Rightarrow $ W = 2Fr $\theta $ ……….. (ii)

Here, total torque can be written as

$\tau $ = F × r + F × r = 2Fr ……. (iii)

From (ii) and (iii)

W = $\tau $ $\theta $……….. (iv),

This is the required expression for work done by the couple.

Power:

Now, differentiation equation (iv) with respect to time.

$\frac{dW}{dt}$ = $\frac{d\,(\tau \,\theta )}{dt}$

Or, P = $\tau $.$\frac{d\theta }{dt}$= $\tau $ $\omega $

$\therefore $ P = $\tau $ $\omega $, which is the required expression for power of couple.

Total kinetic Energy of a Rolling Body:

Let us consider a spherical rigid body of mass m, moment of inertia I and radius ‘R’ is rolling with linear velocity ‘v’ and angular velocity ‘$\omega $’ on a horizontal track as shown in figure above. Let ‘K’ be the radius of gyration of the given rigid body. The total kinetic energy of the rolling body in the sum of translational K.E. and rotational K.E., i.e.

K.E_total = K.E_tans+ K.E._rot

K.E_total = $\frac{\mathbf{1}}{\mathbf{2}}$mv² + $\frac{\mathbf{1}}{\mathbf{2}}$I$\omega $²

In terms of radius of gyration, moment of inertia can be expressed as

I = mK²

$\therefore $ K.E._toal . $\frac{1}{2}$mV² + $\frac{1}{2}$mK²$\omega $²

Since, v = $\omega $R $\Rightarrow $ $\omega $ = $\frac{v}{R}$

Then, K.E._total = $\frac{1}{2}$mv² + $\frac{1}{2}$mK² $\frac{{{v}^{2}}}{{{R}^{2}}}$

Or, K.E._total = $\frac{\mathbf{1}}{\mathbf{2}}$mv²$\left( \mathbf{1}+\frac{{{\mathbf{K}}^{\mathbf{2}}}}{{{\mathbf{R}}^{\mathbf{2}}}} \right)$

This is the required expression for total kinetic energy of a rolling body.

Acceleration of a Rolling body along an Inclined plane:

Let us consider a spherical body of mass ‘m’ and radius ‘R’ that starts to roll down along an inclined plane. Let ‘h’ be the height and ‘s’ be the length of the inclined plane which makes an angle $\theta $ with the horizontal. If the object rolls down from rest its initial velocity, (u) is equal to zero. When the object rolls down, it loses its potential energy and gains K.E.

From the conservation of mechanical energy gain in K.E. = loss in P.E.

Or, $\frac{1}{2}$mv²$\left( 1+\frac{{{K}^{2}}}{{{R}^{2}}} \right)$= mgh

Or, v² = $\frac{2gh}{1+\frac{{{k}^{2}}}{{{R}^{2}}}}$

Or, v = $\sqrt{\frac{2g\,s\,\sin \theta }{1+\frac{{{K}^{2}}}{{{R}^{2}}}}}$………. (i) [$\because $Sin$\theta $ = h/s → h = s sin$\theta $]

We know,

v² = u² + 2as

Or, $\frac{2g\,s\,\sin \theta }{1+\frac{{{K}^{2}}}{{{R}^{2}}}}$= 0 + 2as

Or, a = $\frac{g\,\,\sin \theta }{1+\frac{{{K}^{2}}}{{{R}^{2}}}}$……… (ii)

This is the required expression for acceleration of a rolling body is an inclined plane.

Time to reach the ground (t):

We have, v = u + at

From equations (i) and (ii),

Or, $\sqrt{\frac{2g\,s\,\sin \theta }{1+\frac{{{K}^{2}}}{{{R}^{2}}}}}$= 0 + $\frac{g\,\,\sin \theta }{1+\frac{{{K}^{2}}}{{{R}^{2}}}}$.t

Squaring both sides

$\frac{2g\,s\,\sin \theta }{1+\frac{{{K}^{2}}}{{{R}^{2}}}}$= $\frac{{{g}^{2}}si{{n}^{2}}\theta }{{{\left( 1+\frac{{{k}^{2}}}{{{R}^{2}}} \right)}^{2}}}$.t²

Or, $\sqrt{\frac{2s(1+{{k}^{2}}/{{R}^{2}})}{gh/s}}$= ts

$\therefore $ t = $\sqrt{\frac{2{{s}^{2}}(1+{{k}^{2}}/{{R}^{2}})}{gh}}$

This is the required expression for time to reach the ground level for a body rolling down an inclined plane.

Numerical Problems [Rotational Dynamics]

(First try yourself, if any confusion see next post for solution)

You will enjoy the numerical problems of rotational dynamics if you are able to compare the rotational motion with linear motion.

Comparison Rotational motion with linear motion


	Translational/Linear Motion	Rotational Motion
1.	Mass, m Unit: kg	Moment of inertia, I = $\Sigma $mr² Unit: kgm²
2.	Linear displacement, s or d Unit: m	Angular displacement, $\theta $ Unit: radian Also, 180^o = 200^g= $\pi $^c
3.	Linear velocity, v = $\frac{s}{t}$ , $\frac{ds}{dt}$ , $\frac{∆s}{∆t}$ Unit: ms^–1	Angular velocity, $\omega $ = $\frac{\theta }{t}$, $\frac{d\theta }{dt}$,$\frac{∆\theta }{∆t}$ Also, v = r $\omega $ Unit: rads^–1
4.	Linear momentum, P = mv Unit: kg m s⁻¹	Angular momentum, L = I $\omega $ Unit: kg m² s⁻¹ Also, L = r × P
5.	Linear acceleration, a = $\frac{dv}{dt}$, $\frac{∆v}{∆t}$, $\frac{v\,-u}{t}$, $\frac{{{\text{v}}_{\text{2}}}\text{-}{{\text{v}}_{\text{1}}}}{\text{t}}$ Unit: ms^–2	Angular velocity, $\alpha $ = $\frac{d\omega }{dt}$, $\frac{{{\omega }_{}}\,-\,{{\omega }_{1}}}{t}$, $\frac{{{\omega }_{2}}\,-\,{{\omega }_{1}}}{t}$ Unit: rad s^–2 Also, a = r $\alpha $
6.	(i) Force, F = ma Also, (ii) F = $\frac{dP}{dt}$ Unit: N	Torque, $\tau $ = I$\alpha $ Also, (ii) $\tau $ = $\frac{dL}{dt}$ (iii) $\tau $ = r × F Unit: Nm
7.	Principle of conservation of Linear momentum, For F_ext= 0, P = constant	Principle of conservation of Angular momentum, For ${{\tau }_{ext}}$ = 0, L = constant (= Iw) i.e. I₁${{\omega }_{1}}$ = I₂${{\omega }_{2}}$
8.	Linear K.E. = $\frac{1}{2}$m v² Unit: J	Rotational K.E. = $\frac{1}{2}$I${{\omega }^{2}}$ Unit: J
9.	Work done, W = F×S Unit: J	Work done, W = $\tau $ × $\theta $ Unit: J
10.	Power P = $\frac{W}{t}$ Also, P = FV Unit: Watt	Power P =$\frac{W}{t}$ Also, P = $\tau $ $\omega $ Unit: Watt
Equations Of Motion
11.	v = u+ a t	$\omega $ = ${{\omega }_{o}}$+ $\alpha $t
12.	v² = u²+ 2as	${{\omega }^{2}}$= ${{\omega }_{o}}^{2}$+ 2$\alpha $$\theta $
13.	s = ut + $\frac{1}{2}$at²	$\theta $ = ${{\omega }_{o}}$t + $\frac{1}{2}$$\alpha $t²

Type – 1 (Conservation of angular momentum)

Angular momentum L = constant (In the absence of external force) I₁${{\omega }_{1}}$ = I₂${{\omega }_{2}}$

I₁${{\omega }_{1}}$ = I₂${{\omega }_{2}}$
$\omega $ = 2$\pi $f
Moment of inertia, I = $\Sigma $mr²

Q.1. A ballet dancer spins with 2.4 rev/s with her arms outstretched when the moment of inertia about the axis of rotation is I. With her arms folded, the moment of inertia about the same axis becomes 0.6I. Calculate the new rate of spin.

[Ans : 4 rev/sec]

Q.2. A ballet dancer spins about a vertical axis at 1 revolution per second with her arms stretched. when the moment of inertia about the axis of rotation is I. With her arms folded the moment of inertia about the axis decreases by 40 %. Calculate the new rate of revolution.

[Ans: 1.667 rev/sec]

Q.3. A disc of moment of inertia 5×10^–4kg m²is rotation freely about its axis through its centre at 40 rpm. Calculate the new revolution per minute if some wax of mass 0.02 kg is dropped gently on the disc 0.08m from the axis.

[Ans: 32 rpm]

Q.4 A Physics teacher stands on a freely rotating platform. He holds a dumbbell in each hand of his outstretched arms while a student gives him a push until his angular velocity reaches 1.5 rad/sec. When the freely spinning teacher pulls his hands in closed to his body, his angular velocity increases to 5.0 rad/sec. What is the ratio of final K.E. to initial K.E.?

Ans: 3.33

Q.5 A playground merry-go-round with a radius of 2.0 m has a moment of inertia of 250 kgm² and is rotating at 10rev/min. A 25 kg child jumps onto the edge of the merry-go-round. What is the new angular speed of the merry-go-round?

[Ans: 7.14 rpm]

Type-2:

Torque, $\tau $ = I$\alpha $
$\omega $ = ${{\omega }_{o}}$+ $\alpha $t
${{\omega }^{2}}$= ${{\omega }_{o}}^{2}$+ 2$\alpha $$\theta $
K.E. = $\frac{1}{2}$I${{\omega }^{2}}$
Total K.E. of a rolling body is given by
1. K.E_total = K.E_tans+ K.E._rot
2. K.E_total = $\frac{1}{2}$mv² + $\frac{1}{2}$I${{\omega }^{2}}$

Q.6. A constant torque of 500 Nm turns a wheel, which has a moment of inertia 20 kgm² about its center. Find the angular velocity gained in 2 second and the kinetic energy gained.

[Ans : 50 rad/sec, 25000 J]

Q.7. A constant torque of 200Nm turns a wheel about its centre. The moment of inertia about this axis is 100 kgm². Find the kinetic energy gained after 20 revolutions when it starts from rest.

[Ans : 22.42 rad/sec, 25132.82 J]

Q. 8. A constant torque of 500Nm turns a wheel about its centre. The moment of inertia about this axis is 100 kgm². Find the angular velocity gained in 4 seconds and kinetic energy gained after 20 revolutions.

[Ans : 20 rad sec^–1, 62831.85 J]

Q.9. A constant torque of 200Nm turns a wheel about its centre. The moment of inertia about this axis is 100 kgm². Find the angular velocity gained in 4 seconds and kinetic energy gained after 10 revolutions.

[Ans: 8 rad/sec, 12566.4 J]

Q.10. A constant torque of 200Nm turns a wheel about its centre. The moment of inertia about this axis is 100 kgm². Find the kinetic energy gained after 20 revolutions.

[Ans: 22.42 rad sec^–1, 25132.82 J]

Q.11. A force of 20N is applied tangentially to a wheel of mass 10 kg and diameter 5m. Calculate the torque applied and angular velocity at the end of 10s?

[Ans 50 Nm , 16 rad/s]

Q. 12. A disc of radius 1 m and mass 5 kg is rolling along a horizontal plane. Its moment of inertia about its centre 2.5 kg m². If its velocity along the plane is 2 ms^–1, find its angular velocity and the total energy.

[Ans:2 rad/sec, 15 J]

Solution:

Type-3:

Angular acceleration, $\alpha $ = $\frac{{{\omega }_{2}}-{{\omega }_{1}}}{t}$
$\theta $ = $\omega $_ot + $\frac{1}{2}$$\alpha $t²
$\omega $ = $\omega $_o+ $\alpha $t
Torque, $\tau $ = I $\alpha $

Q.13. An electric fan is turned off and its angular velocity decreases from 500 rev/min to 200 rev/min in 4 seconds. Find the angular acceleration and the number of revolutions made by the motor in 4 sec interval?

[Ans: -7.85 rad/s², 23.34]

Q.14. An electric fan is turned off, and its angular velocity decreases uniformly from 500 rev/min to 200 rev/min in 4.00s (a) Find the angular acceleration and the number of revolutions made by the motor in 4.00s interval. (b) How many more seconds are required for the fan to come to rest if the angular acceleration remains constant?

[Ans –7.85 rad s^-2 , 23.33 rev, 2.66 sec.]

Q.15. A flywheel of moment of inertia 0.32 kgm² is rotated steadily at 120 rads^–1 by a 50 watt electric motor, (i) find the kinetic energy of the flywheel (ii) calculate the value of the frictional couple opposing the rotation.

[Ans: 2304 J, , 0.42 Nm]

Q.16. A flywheel has kinetic energy of 200J. Calculate the number of revolutions before coming to rest if a constant opposing couple of 5 Nm is applied to the flywheel. If the moment of inertia of the flywheel about its centre is 4 kgm² , how long does it take to come to rest . [Ans: n = 6.36, t = 8 sec

Q.17. A wheel starts from rest and accelerates with constant angular acceleration to an angular velocity of 15 revolutions per second in 10 seconds. Calculate the angular acceleration and angle which the wheel has rotated at the end of 2 second.

[Ans : 9.42 rad/sec², 18.84 radian]

Q.18. A computer disc drive is turned on starting from the rest and has constant angular acceleration, (a) how long did it take to make complete rotation and (b) what is its angular acceleration? Given that the disc took 0.750 sec for the drive to make its second revolution.

[Ans: 1.81 sec, 3.83 rad sec^–2]

Q.19. Speed of a body spinning about an axis increases from rest to 100 rev. min^–1in 5 sec, if a constant torque of 20 Nm is applied. The external torque is then removed and the body comes to rest in 100 sec. due to friction. Calculate the frictional torque.

[Ans: 1.002 Nm]

Q.20. A string is wrapped around the rim of a wheel of moment of inertia 0.20 kg m²and radius 20 cm. The wheel is free to rotate about its axis as in figure. Initially, the wheel is at rest. The string is now pulled by a force of 20 N. Find the angular velocity of the wheel after 5.0 s. [100 rad sec^–1]