You will enjoy the numerical problems of rotational dynamics if you are able to compare the rotational motion with linear motion.
Comparison Rotational motion with linear motion
| Translational/Linear Motion | Rotational Motion | |
| 1. | Mass, m Unit: kg | Moment of inertia, I = $\Sigma $mr2 Unit: kgm2 |
| 2. | Linear displacement, s or d Unit: m | Angular displacement, $\theta $ Unit: radian Also, 180o = 200g = $\pi $c |
| 3. | Linear velocity, v = $\frac{s}{t}$ , $\frac{ds}{dt}$ , $\frac{∆s}{∆t}$ Unit: ms–1 | Angular velocity, $\omega $ = $\frac{\theta }{t}$, $\frac{d\theta }{dt}$,$\frac{∆\theta }{∆t}$ Also, v = r $\omega $ Unit: rads–1 |
| 4. | Linear momentum, P = mv Unit: kg m s⁻¹ | Angular momentum, L = I $\omega $ Unit: kg m² s⁻¹ Also, L = r × P |
| 5. | Linear acceleration, a = $\frac{dv}{dt}$, $\frac{∆v}{∆t}$, $\frac{v\,-u}{t}$, $\frac{{{\text{v}}_{\text{2}}}\text{-}{{\text{v}}_{\text{1}}}}{\text{t}}$ Unit: ms–2 | Angular velocity, $\alpha $ = $\frac{d\omega }{dt}$, $\frac{{{\omega }_{}}\,-\,{{\omega }_{1}}}{t}$, $\frac{{{\omega }_{2}}\,-\,{{\omega }_{1}}}{t}$ Unit: rad s–2 Also, a = r $\alpha $ |
| 6. | (i) Force, F = ma Also, (ii) F = $\frac{dP}{dt}$ Unit: N | Torque, $\tau $ = I$\alpha $ Also, (ii) $\tau $ = $\frac{dL}{dt}$ (iii) $\tau $ = r × F Unit: Nm |
| 7. | Principle of conservation of Linear momentum, For Fext = 0, P = constant | Principle of conservation of Angular momentum, For ${{\tau }_{ext}}$ = 0, L = constant (= Iw) i.e. I1${{\omega }_{1}}$ = I2${{\omega }_{2}}$ |
| 8. | Linear K.E. = $\frac{1}{2}$m v2 Unit: J | Rotational K.E. = $\frac{1}{2}$I${{\omega }^{2}}$ Unit: J |
| 9. | Work done, W = F×S Unit: J | Work done, W = $\tau $ × $\theta $ Unit: J |
| 10. | Power P = $\frac{W}{t}$ Also, P = FV Unit: Watt | Power P =$\frac{W}{t}$ Also, P = $\tau $ $\omega $ Unit: Watt |
| Equations Of Motion | ||
| 11. | v = u+ a t | $\omega $ = ${{\omega }_{o}}$+ $\alpha $t |
| 12. | v2 = u2+ 2as | ${{\omega }^{2}}$= ${{\omega }_{o}}^{2}$+ 2$\alpha $$\theta $ |
| 13. | s = ut + $\frac{1}{2}$at2 | $\theta $ = ${{\omega }_{o}}$t + $\frac{1}{2}$$\alpha $t2 |
Type – 1 (Conservation of angular momentum)
Angular momentum L = constant (In the absence of external force) I1${{\omega }_{1}}$ = I2${{\omega }_{2}}$
- I1${{\omega }_{1}}$ = I2${{\omega }_{2}}$
- $\omega $ = 2$\pi $f
- Moment of inertia, I = $\Sigma $mr2
Q.1. A ballet dancer spins with 2.4 rev/s with her arms outstretched when the moment of inertia about the axis of rotation is I. With her arms folded, the moment of inertia about the same axis becomes 0.6I. Calculate the new rate of spin. [Ans : 4 rev/sec]
Solution:
Here,
Csae-1:
Frequency, f1 = 2.4 rps
Moment of inertia, I1 = I
Csae-2:
Moment of inertia, I2 = 0.6I
Frequency, f2 = ?
Form principle of conservation of angular momentum.
I1${{\omega }_{1}}$ = I2${{\omega }_{2}}$
Or, I1 × 2$\pi $f1 = I2 ×2$\pi $f2
Or, f2 = $\frac{{{I}_{1}}.{{f}_{1}}}{{{I}_{2}}}$= $\frac{I\times 2.4}{0.6I}$= 4 rps
$\therefore $ The new rate of her spin is 4rps.
Q.2. A ballet dancer spins about a vertical axis at 1 revolution per second with her arms stretched. when the moment of inertia about the axis of rotation is I. With her arms folded the moment of inertia about the axis decreases by 40 %. Calculate the new rate of revolution. [Ans: 1.667 rev/sec]
Solution:
Here,
Csae-1:
Frequency, f1 = 1 rps
Moment of inertia, I1 = I (say)
Csae-2:
Frequency, f2 = ?
Moment of inertia, I2 = I1 – 40% of I1
Or, I2 = I1 – $\frac{40}{100}$ × I1 = 0.6 I
Form principle of conservation of angular momentum.
I1${{\omega }_{1}}$ = I2${{\omega }_{2}}$
Or, I1 × 2$\pi $f1 = I2 ×2$\pi $f2
$\therefore $ f2 =$\frac{{{I}_{1}}.{{f}_{1}}}{{{I}_{2}}}$= $\frac{I\times 1}{0.6I}$= 1.667 rps
Q.3. A disc of moment of inertia 5×10–4 kg m2 is rotation freely about its axis through its centre at 40 rpm. Calculate the new revolution per minute if some wax of mass 0.02 kg is dropped gently on the disc 0.08m from the axis. [Ans: 32 rpm]
Solution:
Here,
Case-1:
Moment of inertia, I1 = 5×10–4 kg m2
Frequency, f1 = 40 rpm
Case-2:
Frequency, f2 = ?
Mass of wax, m = 0.02 kg
Perpendicular distance from axis of rotation, r = 0.08 m
When some wax is dropped gently on the disc then
New moment of inertia, I2 = I1 + mr2
Or, I2 = 5×10–4 + 0.02 × (0.08)2 = 6.28×10–4 kg m2
Form principle of conservation of angular momentum.
I1${{\omega }_{1}}$ = I2${{\omega }_{2}}$
Or, I1 × 2$\pi $f1 = I2 ×2$\pi $f2
$\therefore $ f2 = $\frac{{{I}_{1}}.{{f}_{1}}}{{{I}_{2}}}$=$\frac{5\times {{10}^{4}}\times 40}{6.28\times {{10}^{4}}}$= 31.85 rpm
Q.4 A Physics teacher stands on a freely rotating platform. He holds a dumbbell in each hand of his outstretched arms while a student gives him a push until his angular velocity reaches 1.5 rad/sec. When the freely spinning teacher pulls his hands in closed to his body, his angular velocity increases to 5.0 rad/sec. What is the ratio of final K.E. to initial K.E.?
Ans: 3.33
Q.5 A playground merry-go-round with a radius of 2.0 m has a moment of inertia of 250 kgm2 and is rotating at 10rev/min. A 25 kg child jumps onto the edge of the merry-go-round. What is the new angular speed of the merry-go-round?
[Ans: 7.14 rpm]
Type-2:
- Torque, $\tau $ = I$\alpha $
- $\omega $ = ${{\omega }_{o}}$ + $\alpha $t
- ${{\omega }^{2}}$= ${{\omega }_{o}}^{2}$ + 2$\alpha $$\theta $
- K.E. = $\frac{1}{2}$I${{\omega }^{2}}$
- Total K.E. of a rolling body is given by
- K.Etotal = K.Etans+ K.E.rot
- K.Etotal = $\frac{1}{2}$mv2 + $\frac{1}{2}$I${{\omega }^{2}}$
Q.6. A constant torque of 500 Nm turns a wheel, which has a moment of inertia 20 kgm2 about its center. Find the angular velocity gained in 2 second and the kinetic energy gained. [Ans : 50 rad/sec, 25000 J]
Solution:
Here,
Torque, $\tau $ = 500 Nm
Moment of inertia, I = 20 kg m2
Time, t = 2 sec
(i) K.E. gained = ?
We have,
Torque, $\tau $ = I$\alpha $
$\alpha $ = $\frac{\tau }{I}$ = $\frac{500}{20}$ = 25 rad sec–2
Now
$\omega $ = $\omega $o + $\alpha $t
For gain, we can take initial angular velocity as zero.
$\omega $ = $\alpha $t = 25 × 2 = 50 rad sec–1
Again K.E. gained = $\frac{1}{2}$I $\omega $2
$\therefore $ K.E. gained = $\frac{1}{2}$×20× 502 = 25000 J
Q.7. A constant torque of 200Nm turns a wheel about its centre. The moment of inertia about this axis is 100 kgm2. Find the kinetic energy gained after 20 revolutions when it starts from rest. [Ans : 22.42 rad/sec, 25132.82 J]
Solution:
Here,
Torque, $\tau $ = 200 Nm
Moment of inertia, I = 100 kgm2
K.E. gained = ? after n = 20 revolutions
Torque, $\tau $= I$\alpha $
Or, $\alpha $ = $\frac{\tau }{I}$= $\frac{200}{100}$ = 2 rad sec–2
Now, $\omega $2 = $\omega $o2 + 2$\alpha $$\theta $
$\omega $2 = 2$\alpha $ ×n ×2$\pi $ [since, $\theta $ = n × 2$\pi $ ]
$\omega $ = $\sqrt{2\times 2\times 20\times 2\pi }$ = 22.42 rad sec–1
Then, K.E. gained = $\frac{1}{2}$I $\omega $2 – $\frac{1}{2}$I $\omega $o2
$\therefore $ K.E. gained = $\frac{1}{2}$×100× 22.422 = 25132.82 J
Q. 8. A constant torque of 500Nm turns a wheel about its centre. The moment of inertia about this axis is 100 kgm2. Find the angular velocity gained in 4 seconds and kinetic energy gained after 20 revolutions. [Ans : 20 rad sec–1, 62831.85 J]
Solution:
Here,
Torque, $\tau $ = 500 Nm
Moment of inertia, I = 100 kgm2
(i) Angular velocity gained (in t = 4 sec), $\omega $ = ?
(ii) K.E. gained = ? after n = 20 revolutions
Torque, $\tau $ = I$\alpha $
Or, $\alpha $ = $\frac{\tau }{I}$= $\frac{500}{100}$ = 5 rad sec–2
Now, $\omega $ = $\omega $o + $\alpha $t
For gain, we can take initial angular velocity as zero.
$\therefore $ $\omega $ = $\alpha $t = 5 × 4 = 20 rad sec–1
And
K.E. gained = $\frac{1}{2}$I$\omega $2 – $\frac{1}{2}$I$\omega $o2 ……..(i)
Angular velocity gained in n = 20 revolutions
$\omega $2 = $\omega $o2 + 2$\alpha $$\theta $
$\omega $2 = 2$\alpha $ × n ×2$\pi $ [since, $\theta $ = n×2$\pi $ ]
$\omega $ = $\sqrt{2\times 5\times 20\times 2\pi }$ = $\sqrt{400\pi }$ rad sec–1
From equation (i),
$\therefore $ K.E. gained = $\frac{1}{2}$×100 × ($\sqrt{400\pi }$)2 = 62831.85 J
Q.9. A constant torque of 200Nm turns a wheel about its centre. The moment of inertia about this axis is 100 kgm2. Find the angular velocity gained in 4 seconds and kinetic energy gained after 10 revolutions. [Ans: 8 rad/sec, 12566.4 J]
Solution:
Here,
Torque, $\tau $ = 200 Nm
Moment of inertia, I = 100 kgm2
(i) Angular velocity gained (in t = 4 sec) = ?
(ii) K.E. gained = ? after n = 10 revolutions
Torque, $\tau $ = I$\alpha $
Or, $\alpha $ = $\frac{\tau }{I}$= $\frac{200}{100}$ = 2 rad sec–2
Now, $\omega $ = $\omega $o + $\alpha $t
For gain, we can take initial angular velocity ($\omega $o) as zero.
$\therefore $ $\omega $ = $\alpha $t = 2 × 4 = 8 rad sec–1
And
K.E. gained = $\frac{1}{2}$I$\omega $2 – $\frac{1}{2}$I$\omega $o2 ……..(i)
Angular velocity gained in n = 20 revolutions
$\omega $2 =$\omega $o2 + 2$\alpha $$\theta $
Or, $\omega $2 = 0 + 2$\alpha $×n ×2$\pi $ [since, $\theta $ = n × 2$\pi $ ]
Or, $\omega $ = $\sqrt{2\times 2\times 10\times 2\pi }$ =$\sqrt{80\pi }$ rad sec–1
From equation (i),
$\therefore $ K.E. gained = $\frac{1}{2}$×100 × ($\sqrt{80\pi }$)2 = 12566.4 J
Q.10. A constant torque of 200Nm turns a wheel about its centre. The moment of inertia about this axis is 100 kgm2. Find the kinetic energy gained after 20 revolutions. [Ans: 22.42 rad sec–1, 25132.82 J]
Solution:
Here,
Torque, $\tau $ = 200 Nm
Moment of inertia, I = 100 kgm2
K.E. gained = ? after n = 20 revolutions
Torque, $\tau $ = I $\alpha $
Or, $\alpha $ = $\frac{\tau }{I}$= $\frac{200}{100}$ = 2 rad sec–2
We have,
$\omega $2 = $\omega $o2 + 2$\alpha $$\theta $
$\omega $2 = 2$\alpha $×n ×2$\pi $ [since, $\theta $ = n × 2$\pi $ ]
$\omega $ = $\sqrt{2\times 2\times 20\times 2\pi }$ = 22.42 rad sec–1
Now,
K.E. gained = $\frac{1}{2}$I$\omega $2 – $\frac{1}{2}$I$\omega $o2 = $\frac{1}{2}$I$\omega $2 – 0
$\therefore $ K.E. gained = $\frac{1}{2}$×100× 22.422 = 25132.82 J
Q.11. A force of 20N is applied tangentially to a wheel of mass 10 kg and diameter 5m. Calculate the torque applied and angular velocity at the end of 10s?
[Ans 50 Nm , 16 rad/s]
Q. 12. A disc of radius 1 m and mass 5 kg is rolling along a horizontal plane. Its moment of inertia about its centre 2.5 kg m2. If its velocity along the plane is 2 ms–1, find its angular velocity and the total energy. [Ans:2 rad/sec, 15 J]
Solution:
Here,
Radius, r = 1 m
Mass, m = 5 kg
Moment of inertia, I = 2.5 kgm2
Linear velocity, v = 2 ms–1
(i) Angular velocity, $\omega $ = ?
(ii) Total energy = ?
We have,
(i) v = $\omega $r
Or, $\omega $ = $\frac{v}{r}$= $\frac{2}{1}$= 2 rad sec–1
(ii) Total K.E. of a rolling body is given by
K.Etotal = K.Etans+ K.E.rot
Or, K.Etotal = $\frac{1}{2}$mv2 + $\frac{1}{2}$I$\omega $2
Or, K.Etotal = $\frac{1}{2}$ × 5 × 22 + $\frac{1}{2}$ × 2.5 × 22
$\therefore $ K.Etotal = 10 + 5 = 15 J
Type-3:
- Angular acceleration, $\alpha $ = $\frac{{{\omega }_{2}}-{{\omega }_{1}}}{t}$
- $\theta $ = $\omega $ot + $\frac{1}{2}$$\alpha $t2
- $\omega $ = $\omega $o + $\alpha $t
- Torque, $\tau $ = I $\alpha $
Q.13. An electric fan is turned off and its angular velocity decreases from 500 rev/min to 200 rev/min in 4 seconds. Find the angular acceleration and the number of revolutions made by the motor in 4 sec interval? [Ans: -7.85 rad/s2 , 23.34]
Solution:
Here,
Initial frequency, f1 = 500 rpm = $\frac{500}{60}$rps = $\frac{25}{3}$ rps
Final frequency, f2 = 200 rpm = $\frac{200}{60}$rps = $\frac{10}{3}$rps
Time interval, t = 4sec
(a) Angular acceleration, $\alpha $ = ?
(b) Number of revolutions (in 4 sec), n = ?
We know,
(a) Angular acceleration, $\alpha $ = $\frac{{{\omega }_{2}}-{{\omega }_{1}}}{t}$
Or, $\alpha $ = $\frac{2\pi {{f}_{2}}-2\pi {{f}_{1}}}{t}$
Or, $\alpha $ = $\frac{2\pi ({{f}_{2}}-{{f}_{1}})}{t}$
Or, $\alpha $ = $\frac{2\pi (10/3-25/3)}{4}$
$\therefore $ $\alpha $ = -7.85 rad/s2
Now, Angular displacement made in 4 sec
$\theta $ = $\omega $1t + $\frac{1}{2}$$\alpha $t2
Or, $\theta $ = 2$\pi $ f1 ×t + $\frac{1}{2}$$\alpha $t2
Or, $\theta $ = 2$\pi $ $\frac{25}{3}$×4 + $\frac{1}{2}$(–7.85) ×42 = 146.64 rad
$\therefore $ Number of revolution (n) = $\frac{\theta }{2\pi }$= 23.34
Q.14. An electric fan is turned off, and its angular velocity decreases uniformly from 500 rev/min to 200 rev/min in 4.00s (a) Find the angular acceleration and the number of revolutions made by the motor in 4.00s interval. (b) How many more seconds are required for the fan to come to rest if the angular acceleration remains constant?
[Ans –7.85 rad s-2 , 23.33 rev, 2.66 sec.]
Q.15. A flywheel of moment of inertia 0.32 kgm2 is rotated steadily at 120 rads–1 by a 50 watt electric motor, (i) find the kinetic energy of the flywheel (ii) calculate the value of the frictional couple opposing the rotation.
[Ans: 2304 J, , 0.42 Nm]
Q.16. A flywheel has kinetic energy of 200J. Calculate the number of revolutions before coming to rest if a constant opposing couple of 5 Nm is applied to the flywheel. If the moment of inertia of the flywheel about its centre is 4 kgm2 , how long does it take to come to rest . [Ans: n = 6.36, t = 8 sec
Q.17. A wheel starts from rest and accelerates with constant angular acceleration to an angular velocity of 15 revolutions per second in 10 seconds. Calculate the angular acceleration and angle which the wheel has rotated at the end of 2 second. [Ans : 9.42 rad/sec2, 18.84 radian]
Solution:
Here,
Initial frequency, f1 = 0 rps
Final frequency, f2 = 15 rps
Time interval, t = 10 sec
(a) Angular acceleration, $\alpha $ = ?
(b) Angle through the wheel has rotated (in 2 sec), $\theta $ = ?
We know,
(a) Angular acceleration, $\alpha $ = $\frac{{{\omega }_{2}}-{{\omega }_{1}}}{t}$
Or, $\alpha $ = $\frac{2\pi {{f}_{2}}-2\pi {{f}_{1}}}{t}$
Or, $\alpha $ = $\frac{(2\pi {{f}_{2}}-0)}{t}$
Or, $\alpha $ = $\frac{2\pi \times 15}{10}$
$\therefore $ Angular acceleration, $\alpha $ = 9.42 rad/s2
Now, Angular displacement made in 2 sec
$\theta $ = $\omega $1t + $\frac{1}{2}$$\alpha $t2
Or, $\theta $ = 2$\pi $ f1 ×t + $\frac{1}{2}$$\alpha $t2
$\therefore $ $\theta $ = 0 + $\frac{1}{2}$(9.42) ×22 = 18.84 rad
Q.18. A computer disc drive is turned on starting from the rest and has constant angular acceleration, (a) how long did it take to make complete rotation and (b) what is its angular acceleration? Given that the disc took 0.750 sec for the drive to make its second revolution. [Ans: 1.81 sec, 3.83 rad sec–2]
Solution:
Here,
Initial angular velocity, $\omega $0 = 0 rad/sec
Let time to complete first revolution is t1
Then (a) t1 = ?
(b) Angular acceleration, α = ?
And let time to complete second revolution is t2, here t2 = 0.750 sec (given)
We know,
$\theta $ = $\omega $ot + $\frac{1}{2}$$\alpha $t2
For one complete revolution, $\theta $ = 2$\pi $
So from above equation
2$\pi $= $\frac{1}{2}$$\alpha $t12………….. (i)
For two complete revolutions, θ = 4π
$\therefore $ 4$\pi $ = $\frac{1}{2}$$\alpha $ (t1 + t2)2 …………. (ii)
Dividing (ii) by (i)
Or, 2 = ${{\left( \frac{{{t}_{1}}+{{t}_{2}}}{{{t}_{1}}} \right)}^{2}}$
Or, 2 = ${{\left( \frac{{{t}_{1}}+0.75}{{{t}_{1}}} \right)}^{2}}$
Or, $\sqrt{2}$ = $\left( \frac{{{t}_{1}}+0.75}{{{t}_{1}}} \right)$
Or, $\sqrt{2}$ t1 = t1 + 0.75
Or, t1 ($\sqrt{2}$–1) = 0.75
Or, t1 = $\frac{0.75}{\sqrt{2}\text{ –1}}\text{ }$
$\therefore $ time to complete first revolution = 1.81 sec
Equation (i) becomes,
$\alpha $ = $\frac{4\pi }{{{t}_{1}}^{2}}$= 3.83 rad/s2
$\therefore $ The angular acceleration is 3.83 rad/s2
Q.19. Speed of a body spinning about an axis increases from rest to 100 rev. min–1 in 5 sec, if a constant torque of 20 Nm is applied. The external torque is then removed and the body comes to rest in 100 sec. due to friction. Calculate the frictional torque. [Ans: 1 Nm]
Solution:
Here,
Initial frequency, f1 = 0 rpm (starting from rest)
After t1 = 5 sec, frequency, f2 = 100 rpm = $\frac{100}{60}$rps
Torque, $\tau $ = 20 Nm
After time interval, t2 = 100 sec
Final frequency, f3 = 0 rpm = 0 rps
Frictional torque, ${{\tau }_{F}}$ = ?
We know,
(a) Angular acceleration, $\alpha $ = $\frac{{{\omega }_{2}}-{{\omega }_{1}}}{t}$
Or, $\alpha $ = $\frac{2\pi {{f}_{2}}-2\pi {{f}_{1}}}{t}$
Or, $\alpha $ =$\frac{2\pi {{f}_{2}}-0}{t}$
Or, $\alpha $ = $\frac{2\pi }{5}$×$\frac{100}{60}$
Or, $\alpha $ = 2.094 rad/s2
Now,
Torque, $\tau $ = I$\alpha $
Or, I = $\frac{\tau }{\acute{a}}$= $\frac{20}{2.094}$ = 9.55 kgm2
Again, when torque is removed the body comes to rest in 100 sec
Then angular retardation due to friction
$\alpha $r = $\frac{{{\omega }_{3}}-{{\omega }_{2}}}{{{t}_{2}}}$
Or, $\alpha $r = $\frac{2\pi {{f}_{3}}-2\pi {{f}_{2}}}{{{t}_{2}}}$
Or, $\alpha $r =$\frac{0-2\pi {{f}_{2}}}{{{t}_{2}}}$
Or, $\alpha $r = – $\frac{2\pi }{100}$ × $\frac{100}{60}$
Or, $\alpha $r = – 0.105 rad sec–2
$\therefore $ Frictional torque, ${{\tau }_{F}}$ = I$\alpha $r = 9.55 × 0.105 = 1.002 Nm
Q.20. A string is wrapped around the rim of a wheel of moment of inertia 0.20 kg m2 and radius 20 cm. The wheel is free to rotate about its axis as in figure. Initially, the wheel is at rest. The string is now pulled by a force of 20 N. Find the angular velocity of the wheel after 5.0 s. [100 rad sec–1]
Solution:
Here,
Moment of inertia, I = 0.2 kgm2
Radius, r = 20 cm = 0.2 m
Initial angular velocity, ωo = 0 rad/sec (rest)
Force, F = 20 N
Angular velocity gained $\omega $ = ? (After t = 5 sec)
We have,
Torque, $\tau $ = I$\alpha $
Or, F × r = I$\alpha $ [Since, $\tau $ = F × r]
Or, $\alpha $ = $\frac{F\times r}{I}$= $\frac{20\times 0.2}{0.2}$ = 20 rad sec–2
Now, $\omega $ =$\omega $o + $\alpha $t
$\omega $ = 0 + $\alpha $t = 20 × 5
$\therefore $ Angular velocity gained, $\omega $ = 100 rad sec–1
MCQ
Rotational Dynamics
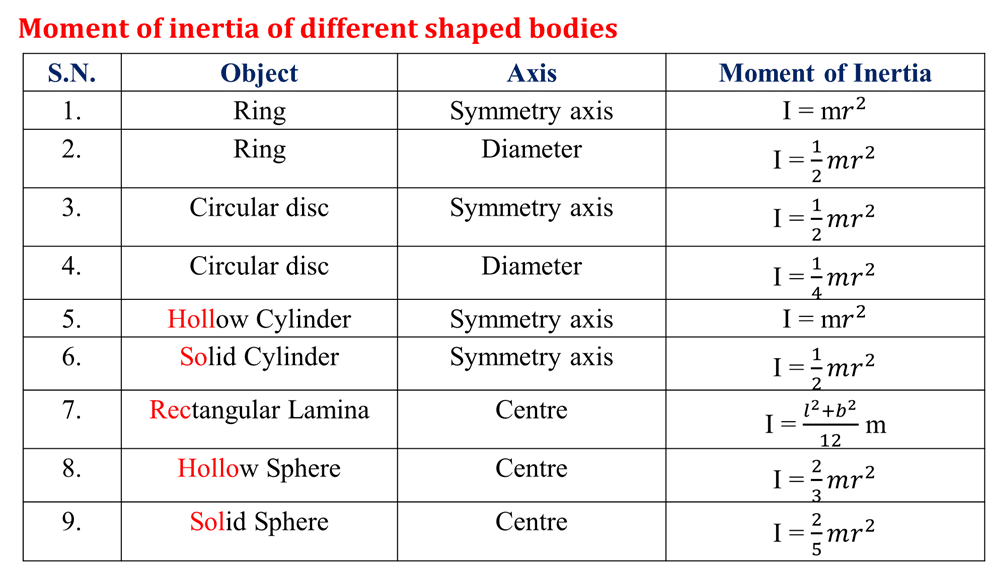
1. Moment of inertia of a body does not depends upon its.
a. mass
b. distribution of mass
c. angular velocity
d. axes of rotation
2. The moment of inertia of a body depends upon
a. distribution of mass
b. angular velocity
c. angular acceleration
d. linear velocity
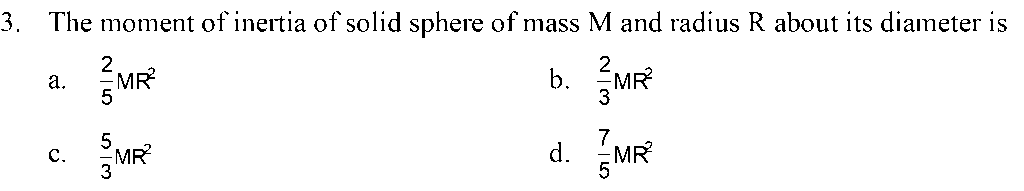
4. The product of moment of inertia and angular velocity is
a. torque
b. work
c. power
d. angular momentum
5. Force in linear motion has its analogue in rotational motion.
a. angular momentum
b. angular velocity
c. torque
d. moment of inertia
6. If torque acting on a system is zero, which of following is conserved
a. force
b. linear momentum
c. angular momentum
d. angular impulse
7. If the rotational kinetic energy of a body is ‘E’ and moment of inertia is ‘I’ then angular momentum will be

8. The moment of linear momentum is called
a. torque b. couple.
c. impulse d. angular momentum
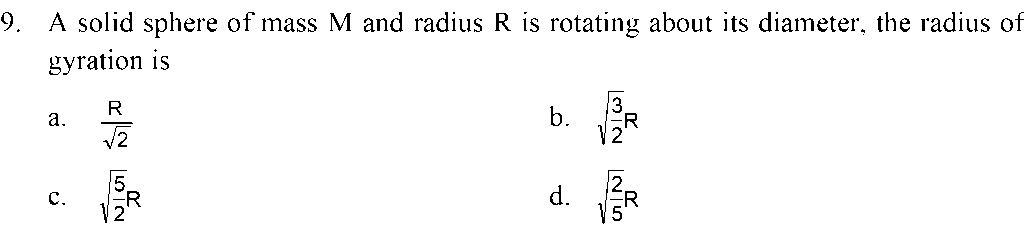
10. For a hollow cylinder and a solid cylinder of the same mass and radius rolling without slipping on an inclined plane, which of these reaches the ground earlier?
a. hollow cylinder
b. solid cylinder
c. both simultaneously
d. cannot say anything
11.

(a) Rotational kinetic energy (b) Torque (c) Power (d) Potential energy
12. When a body rolls down an inclined plane, the total potential energy of the body changes into
a. Rotational K.E.
b.Translational K.E.
c. Both rotational and translational K.E
d.None
13. The product of moment of inertia and angular acceleration gives
a. Linear momentum
b. Angular momentum
c. Torque
d. Force
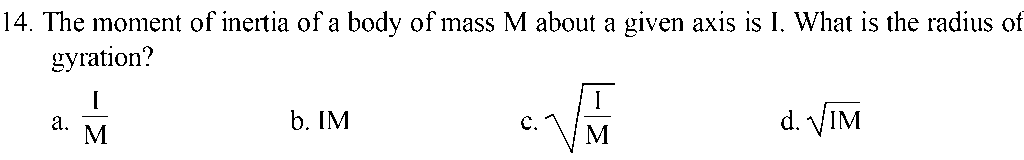
15. A flywheel rotates at a constant speed of 3000 rpm. The angle described by the shift in radian in 1 sec is:
(a) 2p (b) 20p (c) 100p (d) 3000p
16. A disc and ring have same mass and same radius. If we denote the moment of inertia of disc by Id and that of ring by Ir , then:
a. Ir > Id
b. Ir < Id
c. Ir = Id
d. Their relation depends upon the nature of material
17. A dancer on ice spins faster, when she folds her arms. This is due to
a. Increase in energy & momentum
b. Decrease in friction
c. Constant angular momentum and increases in KE
d. Increases in energy and decrease in angular momentum
18. The unit of radius of gyration is
a. radian
b.meter
c. radian/sec
d. meter/sec
19. The spokes are used in bicycle wheel to
a. Increases frictional force
b. Decreases frictional force
c. Increases moment of inertia
d. Increase angular momentum
20. A ring, a disc, solid sphere, hollow sphere are dropped from the same inclined plane of same height then which one of the following reaches the ground first
a. Ring b. Disc
c. Solid sphere d. Hollow sphere
Answer Key of MCQ
| 1. c | 2. a | 3. a | 4. d | 5. c | 6. c | 7. b | 8. d | 9. d | 10. b |
| 11. a | 12. c | 13. c | 14. c | 15. c | 16. a | 17. c | 18. b | 19. c | 20. c |
dai heat and thermodynamics pani halidinuna
dai heat and thermodynamics pani halidinuna
please post notes and numericals for heat and thermodynamics as well
Please numerical solutions of heat and thermodynamics