Electrical Circuit Class 12 Physics | Notes

Kirchhoff’s laws:

Kirchhoff’s first law / Kirchhoff’s junction law / Kirchhoff’s current (KCL):

It states that, “The algebraic sum of all currents meeting at a junction point in an electrical circuit is zero.” i.e. $\sum{I=0}$

Sign Convention

According to sign convention, current entering to the junction point is taken as positive and the current leaving through the junction point is taken as negative.

i.e. I₁ and I₂ are positive but I₃, I₄ and I₅ are negative.

From Kirchhoff’s first law, we can write

$\sum{I=0}$

Or, I₁ + I₂ + (–I₃) + (–I₄) + (–I₅) = 0

Or, I₁ + I₂ = I₃ + I₄+ I₅

From above result, Kirchhoff’s first law also can be stated as “The sum of all currents entering to the junction point is equal to the sum of all currents leaving through the junction point”. This law is also known as current law or junction law.

The principle of Kirchhoff’s first law is ‘conservation of charge’.

Kirchhoff’s second law / Kirchhoff’s loop law / Kirchhoff’s voltage law (KVL):

It states that, “In any closed loop of electrical circuit, the algebraic sum of emf of all batteries is equal to the algebraic sum of product of current and resistance through which it flows.” 

i.e. $\sum{E=\sum{IR}}$

Sign convention

1. In any closed loop, if the direction of loop is from negative terminal to positive terminal of a battery, the emf is taken as positive and if the direction loop is from positive terminal to negative terminal, the emf is taken as negative.

2 In any closed loop, if the direction of loop is in the direction of flow of current, the product of current and resistance (IR) is taken as positive and if the direction of loop is in the direction opposite to the flow of current, the product of current and resistance is taken as negative. The principle of Kirchhoff’s second law is ‘conservation of energy’.

Explanation

Applying Kirchhoff’s voltage law (KVL) in closed loop ABCFA,

According to sign convention, E₁ is positive but E₂ is negative. Also, I₁R₁ and I₁R₂ are positive but I₂R₃ and I₂R₄ are negative.

Now we can write,

E₁ – E₂ = I₁R₁ + I₁R₂ – I₂R₃ – I₂R₄

Applying Kirchhoff’s voltage law (KVL) in closed loop CDEFC,

According to sign convention, E₂ is positive, I₂R₃, I₂R₄ and (I₁+I₂)R₅ all are Positive. Now, we can write,

E₂ = I₂R₃ + I₂R₄ + (I₁ +I₂)R₅

Wheatstone bridge:

It is an electrical circuit which is used to measure value of unknown resistance.

Principle: “A Wheatstone bridge works on the principle of null deflection.i.e.no current flows through the galvanometer.”

The balanced condition for Wheatstone bridge is

For, I_g = 0, $\frac{P}{Q}=\frac{X}{R}$

Construction:

Fig: Wheatstone bridge

A Wheatstone bridge consists of four resistance P, Q, R and X placed in the form of quadrilateral ABCD as shown in figure above. The resistance ‘P’ and ‘Q’ are fixed value resistance. ‘R’ is variable resistance which is used to change the value of current and ‘X’ is unknown resistance whose value is to be determined. A sensitive galvanometer is connected in between ‘B’ and ‘D’ and the point ‘A’ and ‘C’ are connected with positive and negative terminal of a battery through a key shown in figure above.

Working

When key is closed, an amount of current ‘I’ starts to flow. From point A, the current ‘I’ gets divided into ‘I₁‘ and ‘I₂‘ and flows through resistance P and X respectively. Let ‘I_g‘ be the amount of current flowing through galvanometer (B to D). Then (I₁ – I_g) and (I₂ + I_g) be the amount of current flow through resistance Q and R respectively.

On applying Kirchhoff’s 2^nd law in closed loop ABDA,

I₁P + I_gG – I₂X = 0 …(i)

On applying Kirchhoff’s 2^nd law in closed loop BCDB,

(I₁ – I_g)Q – (I₂ + I_g)R – I_gG = 0 …….(ii)

Wheatstone bridge works on the principle of null deflection i.e. no amount of current flows through the galvanometer. i.e. I_g = 0

Now, equation (i) and (ii) become,

I₁P – I₂X = 0 

Or, I₁P = I₂X …(iii)

and, I₁Q – I₂R = 0

Or, I₁Q = I₂R ….(iv)

Dividing equation (iii) by (iv), we get

$\frac{{{I}_{1}}P}{{{I}_{1}}Q}=\frac{{{I}_{2}}X}{{{I}_{2}}R}$

Or, $\frac{P}{Q}=\frac{X}{R}$ This is the balanced condition of Wheatstone Bridge.

Also, $X=\frac{P}{Q}R$

Now, knowing the values of P, Q and R,  the value of X can be determined.

Meter bridge:

It is an electrical circuit which is used to measure the value of unknown resistance. The wire used in this instrument is exactly one-meter that’s why it’s name is Meter Bridge.

Principle

A meter bridge works upon the principle of balanced condition of Wheatstone bridge i.e. no amount of current flows through the galvanometer. The balanced condition of Wheatstone bridge is

$\frac{P}{Q}=\frac{X}{R}$ ………………..(i)

Construction

Fig: Determination of unknown resistance using meter bridge

A meter bridge consists of a uniform wire AC of length one meter (100cm) made up of manganin or constantan having high melting point and low value of temperature coefficient. The wire AC is stretched between two points on a wooden board provided with two L-shaped copper stripe. Another copper stripe is fitted between two L-shaped copper stripe providing with two gaps. A variable resistance ‘R’ is placed in right gap and unknown resistance ‘X’ is placed in left gap whose value is to be determined. One end of a sensitive galvanometer is connected at a point ‘D’ and another end of galvanometer is connected with a jockey which can freely slide on the wire of meter bridge. The end ‘A’ is connected with positive terminal and ‘C’ is connected with negative terminal of a battery through a key (K). A meter scale is placed parallel to the length of wire. 

Working

When key is closed, an amount of current starts to flow. When the Jockey is placed in contact with wire AC, the galvanometer shows deflection. On sliding the Jockey on the wire AC, suppose at any point B at a distance l from A, the galvanometer shows null deflection. Let AB = l cm and BC =(100 – l) cm.

Let resistance of a wire from A to B is P and from B to C is Q.

Since, we know that resistance of uniform wire is directly proportional to length,

i.e. P $\propto $ l

Or, P = Kl……….(ii)

And, Q $\propto $ (100-l)

Or, Q = K (100-l)……(iiii)

Dividing equation (ii) by (iii) we get,

$\frac{P}{Q}=\frac{l}{(100-l)}$

From equation (i),

$\frac{X}{R}=\frac{l}{(100-l)}$

$X=\frac{l}{(100-l)}R$

This is the required expression to determine the value of unknown resistance.

Potentiometer:

It is an electrical instrument which is used to measure emf of a cell, to compare emf of two cells and to determine internal resistance of a cell.

Construction:

Potentiometer consists of a uniform wire AB of length about 10m made up of constantan or manganin fixed on a wooden board. The end ‘A’ is connected with positive terminal and ‘B’ is connected with negative terminal of driver cell through a key, an ammeter and a variable resistance (Rheostat, R_h) as shown in figure above. The driver cell (accumulator) is used to supply constant amount of current and variable resistance is used to change the value of current. A meter scale is placed parallel to the length of wire.

Principle

The potentiometer works upon the principle that “The potential drop across any portion of the potentiometer wire is directly proportional to the length of that portion. i.e.

V$\propto $l

Or, V = kl

i.e. potential gradient $\frac{V}{l}$= constant.

Explanation:

Let ‘a’ be the area of cross section of potentiometer wire and its resistivity is $\rho $. Let us take a portion of the potentiometer wire of length ‘l’. Now resistance of that portion is

R = $\rho \frac{l}{a}$

When key is closed and amount of current ‘I’ starts to flow through the potentiometer wire. Now, the potential dropped across the portion of length ‘l’ of resistance R is 

V = IR

or, V = I $\times $ $\rho \frac{l}{a}$

or, V = k $\times $ l (where k = $\rho \frac{I}{a}$ are constant)

$\therefore $ V $\propto $ l 

Applications of potentiometer:

1. Comparison of emf of two cells using potentiometer:

Fig: Comparison of emf of two cell using potentiometer

Let us consider a potentiometer of uniform wire AB of length about 10m. The end A of the wire is connected with positive terminal and end B is connected with negative terminal of driver cell through an ammeter, a key and a variable resistance (Rheostat, R_h) as shown in figure above. Let us consider two cell of emf E₁ and E_2, in which the value of E₁is known but E₂ is to be determined. Now, positive terminals of cell E₁ and E₂ are connected with a point A and negative terminals are connected with two-way key as shown in figure. One end of sensitive galvanometer is connected with two-way key and another end is connected with jockey which can freely slide on the wire of potentiometer.

When key K₁ is closed and K₂ is opened, on doing so the circuit will be open for cell E₂. On sliding the jockey on the potentiometer wire, let at any point C at distance l₁ from A, the galvanometer shows null deflection. Let V_AC be the potential across AC.

Then for I_g = 0 we can write,

E₁ = V_AC…………(i)

According to the principle of potentiometer, we can write,

V_AC $\propto $ l₁ 

Or, V_AC = Kl₁

Or, E₁ = Kl₁ ……….(ii)

Similarly, when key K₂ is closed and K₁ is opened, on doing so the circuit will be open for cell E₁. On sliding the jockey on the potentiometer wire, let at any point D at distance ‘l₂‘ from A, the galvanometer shows null deflection. Let V_AD be the potential across AD.

Then for I_g = 0 we can write,

E₂ = V_AD…………(iii)

From the principle of potentiometer, we can write,

V_AD $\propto $ l₂ 

Or, V_AD = Kl₂

Or, E₂ = Kl₂ ……….(iv)

Dividing equation (ii) & (iv) we get,

$\frac{{{E}_{1}}}{{{E}_{2}}}=\frac{{{l}_{1}}}{{{l}_{2}}}$

This is the required expression for comparison of emf of two cells using potentiometer.

2. Determination of internal resistance of a cell using potentiometer:

Let us consider a potentiometer of uniform wire AB of length about 10m. The end A of the wire is connected with positive terminal and end B is connected with negative terminal of driver cell through an ammeter, a key and a variable resistance (Rheostat, R_h) as shown in figure above. 

Fig: Determination of internal resistance of a cell using potentiometer

Let us consider an experimental cell of emf ‘E’ has an internal resistance ‘r’. This value of internal resistance ‘r’ is to be determined and also let us take a known value of resistance R (using resistance box R.B.). The positive terminal of the cell and one end of ‘R’ are connected with point ‘A’ and negative terminal of cell and another end of ‘R’ are connected with one end of sensitive galvanometer through two way key K₁ and K₂ respectively. The other end of galvanometer is connected with a jockey which can freely slide on the wire of potentiometer. 

When key K₁ is closed and K₂ is opened, on doing so the circuit will be open for R. On sliding the jockey on the potentiometer wire, let at any point C at distance ‘l₁‘ from A, the galvanometer shows null deflection. Let V_AC be the potential across AC.

Then for I_g = 0 we can write,

E = V_AC…………(i)

According to the principle of potentiometer, we can write,

V_AC $\propto $ l₁ 

Or, V_AC = Kl₁

Or, E = Kl₁ ……….(ii)

Similarly, when key K₁ and K₂ both are closed then on sliding the jockey on the potentiometer wire, let at any point D at distance l₂ from A, the galvanometer shows null deflection. Let V_AD be the potential across AD.

Then I_g = 0 but in this case, an amount of current I flows through the external resistance R and let V ve the potential difference across the resistor R then we can write,

V = V_AD…………(iii)

From the principle of potentiometer, we can write,

V_AD $\propto $ l₂ 

Or, V_AD = Kl₂

Or, V = Kl₂ ……….(iv)

Dividing equation (ii) by (iv) we get,

$\frac{E}{V}=\frac{{{l}_{1}}}{{{l}_{2}}}$

Using circuit i.e. E = I (R+r), above equation becomes

or, $\frac{I\left( R+r \right)}{IR}$ = $\frac{{{l}_{1}}}{{{l}_{2}}}$

or, $\frac{R}{R}+\frac{r}{R}$ = $\frac{{{l}_{1}}}{{{l}_{2}}}$

or, 1 +$\frac{r}{R}$ = $\frac{{{l}_{1}}}{{{l}_{2}}}$

or, $\frac{r}{R}$ = $\frac{{{l}_{1}}}{{{l}_{2}}}$ – 1

$\therefore $ r = $\left( \frac{{{l}_{1}}-{{l}_{2}}}{{{l}_{2}}} \right)R$

This is the required expression for determination of internal resistance using potentiometer.

Now, knowing the values of l₁, l₂ and R, the value of ‘r’ can be determined.

3. Determination (measurement) of emf of a cell using potentiometer:

Fig: Determination of emf of a cell using potentiometer

Let us consider a potentiometer uniform wire AB of length about 10m. The end A of the wire is connected with positive terminal and end B is connected with negative terminal of driver cell through an ammeter, a key and a variable resistance (Rheostat, R_h) as shown in figure above. Let us consider two cell of emf E₁ (unknown and to be determined) and E₂ (known)  _, in which the value of E₁is known but E₂ is to be determined. Now, positive terminals of cell E₁ and E₂ are connected with a point A and negative terminals are connected with two-way key as shown in figure. One end of sensitive galvanometer is connected with two-way key and another end is connected with jockey which can freely slide on the wire of potentiometer.

When key K₁ is closed and K₂ is opened, on doing so the circuit will be open for cell E₂. On sliding the jockey on the potentiometer wire, let at any point C at distance l₁ from A, the galvanometer shows null deflection. Let V_AC be the potential across AC.

Then for I_g = 0 we can write,

E₁ = V_AC…………(i)

According to the principle of potentiometer, we can write,

V_AC $\propto $ l₁ 

Or, V_AC = Kl₁

Or, E₁ = Kl₁ ……….(ii)

Similarly, when key K₂ is closed and K₁ is opened, on doing so the circuit will be open for cell E₁. On sliding the jockey on the potentiometer wire, let at any point D at distance l₂ from A, the galvanometer shows null deflection. Let V_AD be the potential across AD.

Then for I_g = 0 we can write,

E₂ = V_AD…………(iii)

From the principle of potentiometer, we can write,

V_AD $\propto $ l₂ 

Or, V_AD = Kl₂

Or, E₂ = Kl₂ ……….(iv)

Dividing equation (ii) & (iv) we get,

$\frac{{{E}_{1}}}{{{E}_{2}}}=\frac{{{l}_{1}}}{{{l}_{2}}}$

E₁ = $\frac{{{l}_{1}}}{{{l}_{2}}}\times {{E}_{2}}$

Knowing the values of l₁, l₂ and E₁, the value of E₂ can be determined.

Galvanometer:

It is an electrical instrument which is used to detect the flow of current in the circuit. It also gives the direction of current and measures a small amount of current and potential difference. The resistance of the galvanometer is low. It’s symbol is  

Ammeter:

An ammeter is an electrical instrument used to measure the current passing through it. The resistance of the ammeter is very low. It is always connected in the series in the circuit. It’s symbol is 

Voltmeter:

Voltmeter is an electrical instrument used to measure the potential difference across it. The resistance of the voltmeter is very high.  It is always connected in the parallel with the load resistance in the circuit. It’s symbol is

Shunt:

 It is a low value resistance which is connected in parallel with the galvanometer to convert the galvanometer into an ammeter.

Conversion of galvanometer into an ammeter:

Galvanometer is an electrical instrument which is used to detect the flow of current in the circuit. The resistance of the galvanometer is low.

Ammeter is an instrument used to measure the current passing through it. The resistance of the ammeter is very low. It is always connected in the series in the circuit.

Galvanometer is converted into an ammeter by using suitable shunt (a low value resistance) in parallel with it.  

Fig: Conversion of galvanometer into an ammeter

Let us consider a galvanometer of resistance ‘G’ and shows full scale deflection when an amount of current I_g flows through it. We have to convert the galvanometer into an ammeter which can measure current upto ‘I’ ampere. For this, let us connect a shunt ‘S’ (a low value resistance) in parallel with the galvanometer.

The value of shunt is chosen in such a way that only a desirable amount of current I_g flows through the galvanometer and remaining current (I–I_g) flows through the shunt. 

Since, shunt and galvanometer are in parallel combination, 

$\therefore $ p.d. across shunt (S) = p.d. across galvanometer (G) 

Or, (I–I_g).S = I_gG

Or, S = $\frac{I{}_{g}}{I-{{I}_{g}}}$.G

This is the required value of shunt to convert a galvanometer into an ammeter to measure current upto (I) ampere.

Now the resistance of ammeter is the equivalent resistance of parallel combination of shunt and galvanometer

So,

R_A= $\frac{SG}{S+G}$

So, the resistance of ammeter (R_A) is very small (even smaller than G & S). This is the necessary criterion to be an ammeter.

Conversion of galvanometer into voltmeter:

Galvanometer is an electrical instrument which is used to detect the flow of current in the circuit. The resistance of the galvanometer is low.

Voltmeter is an instrument used to measure the potential difference across it. The resistance of the voltmeter is very high. It is always connected in the parallel with the load resistance in the circuit. 

Fig: Conversion of galvanometer into voltmeter

Let us consider a galvanometer of resistance ‘G’ and show full scale deflection when an amount of current I_g flows through it. We have to convert the galvanometer into voltmeter measure to measure potential difference upto V volt. For this, let us connect a high value resistance ‘R’ in series with a galvanometer. Since galvanometer and high value resistance(R) are in series combination, so total resistance becomes R+G

Now,

Potential (V) = I_g(R+G)

Or, $\frac{V}{{{I}_{g}}}$= R+G

Or, R = $\frac{V}{{{I}_{g}}}$– G

Where R is required value of high value resistance to convert a galvanometer into voltmeter to measure potential difference upto V volt.

The resistance of voltmeter R_v = G + R. 

As the value of R is high, so R_v is also high. This is the necessary criterion to be a voltmeter.

Heating effect of current:

When current flows through a conductor, heat develops in it. This effect of current is known as heating effect of current.

When current flows through a conductor, the free electrons of the conductor come in motion and collision takes place between them. Due to the collision moving electrons lose their kinetic energy and some part of their kinetic energy is converted into heat energy.

Joule’s law of heating:

Let us consider a conductor of resistance (R). Let an amount of current (I) is passed through the conductor for time ‘t’. According to Joule’s law of heating, the heat developed in the conductor is

(i) directly proportional to square of magnitude of current flowing through the conductor.

i.e. H $\propto $ I² ………….(i)

(ii) directly proportional to resistance of conductor.

i.e. H $\propto $ R …………..(ii)

(iii) directly proportional to the time for which current is passed through the conductor.

i.e. H $\propto $ t …………..(iii)

On combining (i), (ii) and (iii) we get,

                H $\propto $ I²Rt

                or, H = k I²Rt

Where ‘k’ is proportionality constant and its value is 1 in S.I.

H = I²Rt

The above result also can be written as

H = $\frac{{{I}^{2}}Rt}{J}$, where ‘J’ is Joule’s equivalent and its value is 4.2 joules/calorie.

Derivation for the expression of heat developed in a wire.

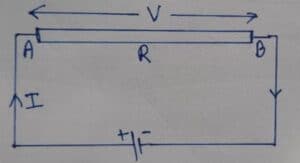
Let us consider a wire AB of resistance R in a circuit as shown in Fig. Let (I) be the steady current passing through it.

In time ‘t’ the  total charge ‘q’ passing through B to A is given by

I = $\frac{q}{t}$

or, q = I.t

Let the potential difference between A and B be (V). Then,

V = IR

The work done to transfer the charge (q) from B to A is given by,

W = qV

From equations (i), (ii) and (iii) we get,

W = I t. I R

Or,  W = I² R t

It the wire is a passive resistor, all the electrical energy is converted into the heat energy, H.

So, W = H and we have,

H =  I²Rt Joule

This is the expression for heat developed in a wire of resistance R.

Electric power:

This is defined as the electrical energy per unit time.

 Mathematically,

Electric power, P = $\frac{H}{t}$ = $\frac{{{I}^{2}}Rt}{t}$

P = I²R ………(i)

P = I×IR

P = IV ………(ii)      Since, V = IR

P = $\frac{V}{R}$ × V       Since,  I = $\frac{V}{R}$

P = $\frac{{{V}^{2}}}{R}$ …………..(iii)

From (i), (ii) and (iii)

P = I²R = IV = $\frac{{{V}^{2}}}{R}$

One unit or 1 kilowatt-hour of electrical energy:

Electric power is defined as the electrical energy per unit time.

Electric power, P = $\frac{Electric\text{ }energy}{time}$

Electric energy = P×t

If P =1 KW and t = 1 hour

Then,

Electric energy = 1 KW × 1 hr

                       = 1 KWhr

                       = 1 unit

Electric energy consumed is said to be one unit if an electric device of 1KW power is used for 1 hour.

Also Read: EMF of a Cell Class 12 Physics | Notes