Magnetic Effect of Current Numericals | Class 12 Physics

Formulae 

Type-One:

1.  Force on a charged particle moving in a uniform magnetic field. (Lorentz force)

F = B q v sin$\theta $

Where 

B = magnetic field

q = charge

V = velocity of the charged particle 

$\theta $ = angle made by $\overrightarrow{B}$ with $\overrightarrow{v}$

In vector form;

$\overrightarrow{F}$ = q ($\overrightarrow{v}$ × $\overrightarrow{B}$)

i.e. force is perpendicular to velocity and magnetic field.

Q.1. A Silver wire has 1×10³⁰ free electrons per cubic meter, a cross sectional area of 2 mm² and carries a current of 5 A. Calculate the force acting on each electron if the wire is now placed in a magnetic field of flux density 0.15 T which is perpendicular to the wire.

Solution:

Here,

Number of free electrons per unit volume, n = 1×10³⁰ m^–3

Area of cross-section, A = 2 mm² = 2×10^–6 m²

Current, I = 5 A

Force, F = ?

Magnetic field, B = 0.15 T

Angle between magnetic field and velocity, $\theta $= 90^o

We have,

F = B q v sin$\theta $ ……(i)

Also,

Current, I = venA

Or, v = $\frac{I}{enA}$

From equation (i)

  F = B q $\frac{I}{enA}$ sin$\theta $  [Here, $\theta $ = 90^o and q = e]

Or, F = Be $\frac{I}{enA}$ × 1

Or, F = 0.15× $\frac{5}{1\times {{10}^{30}}\times 2\times {{10}^{-6}}}$

$\therefore $  F = 3.75×10^–25 N 

Q.2. A copper wire has 10²⁹ free electrons per cubic meter, a cross sectional area of 2mm² and carries a current of 5A. Calculate the force acting on each electron if the wire is now placed in a magnetic field of flux density 0.15T which is perpendicular to the wire.

Solution:

Here,

Number of free electrons per unit volume, n = 1×10²⁹ m^–3

Area of cross-section, A = 2 mm² = 2×10^–6 m²

Current, I = 5 A

Force = ?

Magnetic field, B = 0.15 T

Angle between magnetic field and velocity, $\theta $ = 90^o

We have,

F = B q v sin$\theta $ ……(i)

Also,

Current, I = venA

Or, v = $\frac{I}{enA}$

From equation (i)

F = B q $\frac{I}{enA}$ sin$\theta $  [Here, $\theta $ = 90^o and q = e]

Or, F = Be $\frac{I}{enA}$ × 1

Or, F = 0.15× $\frac{5}{1\times {{10}^{29}}\times 2\times {{10}^{-6}}}$

$\therefore $ F = 3.75×10^–24 N 

Q.3. A copper wire has 1×10²⁹ free electrons per cubic meter and cross-sectional area 2 mm² carries a current of 6 A. Calculate the force acting on each electron if the wire is now placed in a uniform magnetic field of flux density 0.1 T perpendicularly.

Solution:

Here,

Number of free electrons per unit volume, n = 1×10²⁹ m^–3

Area of cross-section, A = 2 mm² = 2×10^–6 m²

Current, I = 6 A

Force = ?

Magnetic field, B = 0.1 T

Angle between magnetic field and velocity, $\theta $ = 90^o

We have,

F = B q v sin$\theta $ ……(i)

Also,

Current, I = venA

Or, v = $\frac{I}{enA}$

From equation (i)

F = B q $\frac{I}{enA}$ sin$\theta $  [Here, $\theta $ = 90^o and q = e]

Or, F = Be $\frac{I}{enA}$ × 1

Or, F = 0.1× $\frac{6}{1\times {{10}^{29}}\times 2\times {{10}^{-6}}}$

$\therefore $ F = 3×10^–24 N 

Q.4. An electron of K.E 10 eV is moving in a circular orbit of radius 11 cm, in a plane at right angle to a uniform magnetic field. Determine the value of flux density. [Mass of an electron = 9.1×10^–31 kg, e = 1.6×10^–19 C]

Solution:

Here,

K.E. of electron = 10 eV

mv² = 10 ×1.6×10^–19 J

v = $\sqrt{\frac{2\times 10\times 1.6\times {{10}^{-19}}}{9.1\times {{10}^{-31}}}}$ ms^–1

Radius, r = 11 cm = 11×10^–2 m

Angle between magnetic field and velocity, $\theta $ = 90^o 

Magnetic field, B = ?

Mass of an electron = 9.1×10^–31 kg

Charge of electron, e = 1.6×10^–19 C

When a charged particle moves in a circular orbit in magnetic field, then magnetic force (Lorentz force)

provides the necessary centripetal force. i.e.

F_B = F_C

Or, B q v sin$\theta $ = $\frac{m{{v}^{2}}}{r}$

Or, B = $\frac{mv}{e\,r\,sin\theta }$

Or, B = $\frac{9.1\times {{10}^{-31}}}{1.6\times {{10}^{-19}}\times 11\times {{10}^{-2}}\times sin{{90}^{o}}}$×$\sqrt{\frac{2\times 10\times 1.6\times {{10}^{-19}}}{9.1\times {{10}^{-31}}}}$

$\therefore $ B = 9.696 T

Type-2:

2. Force on a current carrying conductor placed in uniform magnetic field. 

F = BIl sin$\theta $

Where 

B = magnetic field

I = current

l = length of conductor 

$\theta $ = angle made by $\overrightarrow{B}$ with $\overrightarrow{l}$

In vector form;

$\overrightarrow{F}$ = I ($\overrightarrow{l}$ × $\overrightarrow{B}$)

i.e. force is perpendicular to velocity and magnetic field.

Q.5. A long wire carrying a current of 10A is placed perpendicular to the magnetic field of flux density 5 Tesla. Calculate the force acting on 2m of the wire.

Solution:

Here, 

Current, I = 10 A

Angle between magnetic field and length, $\theta $ = 90^o

Magnetic field, B = 5 T

Force, F = ?

Length of wire, l = 2 m

We have,

F = BIl sin$\theta $

Or, F = 5×10×2×1

Or, F= 100 N

Q.6. A straight conductor of length 5 cm carries a current of 1.5 A. The conductor experiences a magnetic force of 4.5×10^-3 N when it is placed in a magnetic field of 0.9 T. What angle does the conductor make the magnetic field?

Solution:

Here, 

Length of conductor, l = 5 cm = 5×10^–2 m

Current, I = 1.5 A

F_B = 4.5×10^–3 N

Magnetic field, B = 0.9 T

Angle between magnetic field and length, $\theta $ = ?

We have,

F = BIl sin$\theta $

Or, sin$\theta $ = $\frac{F}{BIl}$

Or, $\theta $ = sin^–1 $\left( \frac{F}{BIl} \right)$

Or, $\theta $ = sin^–1 $\left( \frac{4.5\times {{10}^{-3}}}{0.9\times 1.5\times 5\times {{10}^{-2}}} \right)$

$\therefore $ $\theta $ = 3.82^o

Q.7. A wire carrying current of 10 A and 2 m in length is placed in a field of flux density 0.34 T. What is the force on the wire if it is placed at 60^o to the field?

Solution:

Here, 

Current, I = 10 A

Length of wire, l = 2 m

Magnetic field, B = 0.34 T

Force, F = ?

Angle between magnetic field and length, $\theta $ = 60^o

We have,

F = BIl sin$\theta $

Or, F = 0.34×10×2× sin60^o

$\therefore $ F = 5.9 N

Type-3:

3. When a current carrying conductor is placed in a magnetic field it experiences a force (F = BIl sin$\theta $) and the weight of the conductor acts vertically downward. If the arrangement is such that the magnetic force acts in vertically upward direction and if vertically upward force is equal to vertically downward force the condition is known as self-supporting or equilibrium.

For self-supporting 

OR

For equilibrium

OR

For zero tension in the string / spring.

Magnetic force = Weight

F_B = mg

BIl sin$\theta $ = mg

Q.8. A 60cm long wire of mass 10g is suspended horizontally in a transverse magnetic field of flux density 0.4T through two springs at its two ends. Calculate the current required to pass through the wire so that there is zero tension in the springs.  

Solution:

Here, 

Length of wire, l = 0.6 m

Mass of wire, m = 10 g = 10×10^–3 kg

Angle between magnetic field and length, $\theta $ = 90^o

Magnetic field, B = 0.4 T

Current, I = ?

We have,

For zero tension in the string

Magnetic force = Weight

F_B = mg

BIl sin$\theta $ = mg

Or, I = $\frac{mg}{Bl}$ 

Or, I = $\frac{10\times {{10}^{-3}}\times 10}{0.4\times 0.6}$ 

$\therefore $ I = 0.416 A

Q.9. A horizontal straight wire of mass 0.12gm and length 10cm is placed perpendicular to a uniform horizontal magnetic field of flux density 0.6T. If the resistance per unit length of the wire is 3.8$\Omega $m^-1, calculate the potential difference that has to be applied between the ends of the wire to make it just self-supporting.

Solution:

Here, 

Mass of wire, m = 0.12 g = 0.12×10^–3 kg

Length of wire, l = 0.1 m

Angle between magnetic field and length, $\theta $ = 90^o

Magnetic Field, B = 0.6 T

Resistance per unit length, R/l = 3.8 $\Omega $m^–1

Potential difference, V  = ?

We have,

For self-supporting,

Magnetic force = Weight

F_B = mg

BIl sin$\theta $ = mg

Or, I = $\frac{mg}{Bl}$ 

Now,

V = IR

Or, V = $\frac{mg}{Bl}$×R

Or, V = $\frac{mg}{B}$×$\frac{R}{l}$

Or, V = $\frac{0.12\times {{10}^{-3}}\times 10}{0.6}$× 3.8

$\therefore $ V = 0.0076 V

Q.10. A horizontal straight wire 5 cm long weighing 1.2 gm^–1 is placed perpendicular to a uniform horizontal magnetic field of flux density of 0.6 T. If the resistance per unit length of the wire is 3.8 $\Omega $m^–1, calculate the p.d. that has to be applied between the ends of the wire to make it just self-supporting.

Solution:

Here,

Length of wire, l = 5 cm = 5×10^–2 m 

Mass per unit length, $\frac{m}{l}$ = 1.2 g m^–1  = 1.2×10^–3 kg m^–1  

$\therefore $ Total mass of wire, m = $\frac{m}{l}$× l 

$\therefore $ m = 1.2×10^–3 ×5×10^–2 = 6×10^–5 kg

Angle between magnetic field and length,$\theta $ = 90^o

Magnetic Field, B = 0.6 T

Resistance per unit length, $\frac{R}{l}$= 3.8 $\Omega $m^–1

$\therefore $ Total resistance of wire, R = $\frac{R}{l}$× l 

Or, R = 3.8 × 5×10^–2 = 0.19$\Omega $

Potential difference, V = ?

We have,

For self-supporting,

Magnetic force = Weight

F_B = mg

BIl sin$\theta $ = mg

Or, I = $\frac{mg}{Bl}$ 

Now,

V = IR

Or, V = $\frac{mgR}{Bl}$

Or, V = $\frac{6\times {{10}^{-5}}\times 10\times 0.19}{0.6\times 5\times {{10}^{-2}}}$

Or, V = 3.8×10^–3 V

Q.11. A horizontal straight rod of length 20cm and mass 30 gm is placed in a uniform horizontal magnetic field perpendicular to the rod. If a current of 2 A through the rod makes it self-supporting in the magnetic field, calculate the magnetic field. 

Solution:

Here, 

Length of rod, l = 20 cm = 0.2 m

Mass of rod, m = 30 g = 30×10^–3 kg

Angle between magnetic field and length, $\theta $ = 90^o

Current, I = 2 A

Magnetic field, B = ?

We have,

For zero tension in the string

Magnetic force = Weight

F_B = mg

BIl sin$\theta $ = mg

Or, B = $\frac{mg}{Il}$ 

Or, B = $\frac{30\times {{10}^{-3}}\times 10}{2\times 0.2}$

$\therefore $ B = 0.75 T

Type-4:

Biot and Savart Law: 

Biot and Savart Law is used to find the magnitude of magnetic field due to a current carrying conductor of any shape and size.

According to Biot and Savart law, the magnetic field (dB) due to a small current carrying element (dl) is given  by

i.e.  $dB\text{ }\propto \text{ }\frac{I\text{ }dl\text{ }\sin \theta }{{{r}^{2}}}$

Or, $dB\text{  =  }\frac{K\text{ }I\text{ }dl\text{ }\sin \theta }{{{r}^{2}}}$

 Where K is proportionality constant & its value is found to be $\frac{{{\mu }_{0}}}{4\pi }$

$$$dB\text{  = }\frac{{{\mu }_{0}}}{4\pi }\text{ }\frac{\text{ }I\text{ }dl\text{ }\sin \theta }{{{r}^{2}}}$

where ${{\mu }_{0}}$ is magnetic permeability of free of space and its value in SI system is $4\pi \times {{10}^{-7}}H{{m}^{-1}}$

In vector form, the above result can be written as:

$\left[ \overrightarrow{dB}\text{ = }\frac{{{\mu }_{0}}}{4\pi }\text{ I  }\left( \frac{\overrightarrow{dl}\text{ }\times \text{ }\overrightarrow{r}\text{ }}{{{\left| \overrightarrow{r} \right|}^{3}}} \right)\text{  } \right]$

In CGS System, Biot and Savart law can be written as

$\left[ dB\ =\ \frac{I\ dl\ \sin \theta }{{{r}^{2}}} \right]$

Ampere’s Circuital law: 

Ampere’s Circuital law states that “The line integral of the magnetic field in a closed loop is equal ${{\mu }_{o}}$ times the total current enclosed by that loop”. 

i.e. $\oint{\overrightarrow{B}}.\overrightarrow{dl}$ =  ${{\mu }_{o}}I$

Ampere’s circuital law is used to find magnetic fields due to current carrying conductor. 

i.e., objective of Ampere’s circuital law is the same as Biot and Savart law. 

Applications of Biot and Savart Law and Ampere’s Circuital law:

(i) Magnetic field at the centre of current carrying circular coil is

B = $\frac{{{\mu }_{o}}I}{2a}$

Where, ${{\mu }_{o}}$ = Magnetic permeability of free space,

${{\mu }_{o}}$ = 4$\pi $×10^–7 TmA^–1 

I = current

a = radius (r)

For N – Turns, B= $\frac{{{\mu }_{o}}NI}{2a}$

The direction of magnetic field is along the axis of circular coil.

Q.12. A copper wire 28 m long is wound into a flat circular coil 8.0 cm in diameter. If the current of 4.50A flows through the coil, what is the magnetic induction at the centre?

Solution:

Here, 

Length of the wire, l = 28 m

Diameter of the coil, d = 8cm 

Radius of the coil, r = 4×10^–2 m

Current, I = 10A

Magnetic field, B =?

We know,

Total length of wire,  l = No. of turns (N) × circumference (C)

N = $\frac{l}{2\pi r}$…..(i)

Now,

Magnetic field at the centre of current carrying circular coil is

B = $\frac{{{\mu }_{o}}NI}{2r}$ [here, radius, a = r ]

From equation (i),

B = $\frac{{{\mu }_{o}}I}{2r}$× $\frac{l}{2\pi r}$        [Here,${{\mu }_{o}}$ = 4$\pi $×10^–7 TmA^–1 ]

B = $\frac{4\pi \times 10-7\times 4.5}{2\times 4\times 10-2}$× $\frac{28}{2\pi \times 4\times {{10}^{-2}}}$

B = 7.875×10^–3  T.

Q.13. A wire of length 62.8m carrying current 10A is bent into a circular coil of radius 10cm. Calculate the magnetic field at the centre. 

Solution:

Length of wire, l = 62.8m

Current, I = 10A

Radius of coil, r = 10cm = 0.1m

Magnetic field, B = ?

We know,

Total length of wire, l = No. of turns (N) × circumference (C)

N = $\frac{l}{2\pi r}=\frac{62.8}{2\times 3.14\times 0.1}=100$

Now,

Magnetic field, B = $\frac{{{\mu }_{0}}NI}{2r}$

B = $\frac{4\pi \times {{10}^{-7}}\times 100\times 10}{2\times 0.1}$

B =$6.28\times {{10}^{-3}}$T.

Q.14. An electron is revolving around its orbit of radius $5\times {{10}^{-11}}$m with a frequency of $2\times {{10}^{10}}$Hz. Calculate magnitude of magnetic field at its centre.

Solution:

Here,

Radius of orbit, r = $5\times {{10}^{-11}}$m

Frequency, f = $2\times {{10}^{10}}$Hz

Magnetic field at the centre, B = ?

Now,

  Current, I = $\frac{ch\arg e\text{ }(e)}{time\,(t)}$ 

Or, Current, I = $\frac{e}{T}$   

Or, I =  ef     $\because $  Frequency, f = $\frac{1}{Time\,period}$

Or, I =  $1.6\times {{10}^{-19}}\times 2\times {{10}^{10}}$

Or, I = $3.2\times {{10}^{-9}}$A

Now, 

Magnetic field, B = $\frac{{{\mu }_{0}}I}{2r}$

Or, B = $\frac{4\pi \times {{10}^{-7}}\times 3.2\times {{10}^{-9}}}{2\times 5\times {{10}^{-11}}}$

Or, B = $4.02\times {{10}^{-5}}\,$T.

Q.15. An alpha particle makes a full rotation in a circle of radius 1.0 m in 2.0 sec. Calculate the value of magnetic field induction at the centre of the circle. (${{\mu }_{o}}$ = 4$\pi $×10^–7 Hm^–1)

Solution: 

Here, 

Radius of circular path, r = 1 m

Time period, T = 2 sec

Magnetic field, B = ?

_{${{\mu }_{o}}$} = 4$\pi $×10^–7 Hm^–1

For alpha particle, charge, q = +2e

Now,

Magnetic field at the centre of circular current is

B = $\frac{{{\mu }_{o}}I}{2r}$ [here, radius, a = r]

Or, B = $\frac{{{\mu }_{o}}}{2r}$× $\frac{2e}{T}$ [$\because $Current, I = $\frac{q}{t}$= $\frac{2e}{T}$ ]

Or, B = $\frac{4\pi \times {{10}^{-7}}}{2\times 1}$×$\frac{2\times 1.6\times {{10}^{-19}}}{2}$

$\therefore $ B = 1×10^–25  T

2. Magnetic field along the axis of narrow circular coil.

B = $\frac{{{\mu }_{o}}I{{a}^{2}}}{2{{({{a}^{2}}+{{x}^{2}})}^{3/2}}}$ ($\because $ r = $\sqrt{{{a}^{2}}+{{x}^{2}}}$) 

For N- turns

Where,

a is the radius of the circular coil

x is the distance of the point from elementary length dl

B = $\frac{{{\mu }_{o}}NI{{a}^{2}}}{2{{({{a}^{2}}+{{x}^{2}})}^{3/2}}}$

Q.16. A circular coil has 100 turns and a mean diameter of 20 cm. It carries a current of 5 A. Find the strength of the magnetic field at a point on its axis at a distance of 15 cm from the centre of the coil.

Solution:

Here,

Number of turns, N = 100 turns

Diameter of coil, d = 20 cm

Radius of coil, a = 10 cm = 10×10^–2 m

Current, I = 5 A

Magnetic field, B = ?

Axial distance, X = 15 cm= 15×10^–2 m

Magnetic field at the axial point of current carrying circular coil is

B = $\frac{{{\mu }_{o}}NI{{a}^{2}}}{2{{({{a}^{2}}+{{x}^{2}})}^{3/2}}}$ [where ${{\mu }_{o}}$= 4$\pi $×10^–7 Hm^–1]

Or, B = $\frac{4\pi \times {{10}^{-7}}\times 100\times 5\times {{(10\times {{10}^{-2}})}^{2}}}{2{{[{{(10\times {{10}^{-2}})}^{2}}+{{(15\times {{10}^{-2}})}^{2}}]}^{3/2}}}$

$\therefore $ B = 5.36×10^–4 T

Q.17. A coil consisting of 100 circular loop with a radius of 0.6 m carries a current of 5 A. At what distance from the centre, along the axis, the magnetic field magnitude 1/8 as great as it is at the centre?   

Solution:

Here,

Number of turns, N = 100

Radius of coil, a = 0.6 m

Current, I = 5 A

Axial distance, X = ?

Given that

Magnetic field at axial point = $\frac{1}{8}$× Magnetic field at the centre 

Or, $\frac{{{\mu }_{o}}NI{{a}^{2}}}{2{{({{a}^{2}}+{{x}^{2}})}^{3/2}}}$ = $\frac{1}{8}$×$\frac{{{\mu }_{o}}NI}{2a}$

Or, (a² + x² )^3/2 =  8a³

Or, a² + x²  =  8^2/3  (a³)^2/3

Or, x²  =  4a² – a² 

Or, x² = 3a²

Or, x = $\sqrt{3{{a}^{2}}}$

Or, x = $\sqrt{3\times {{0.6}^{2}}}$

Or, x = 1.039 m

3. Magnetic field due to a long current carrying solenoid.

B = ${{\mu }_{o}}$n I

Where, ${{\mu }_{o}}$ = Magnetic permeability of free space,

_{${{\mu }_{o}}$} = 4$\pi $×10^–7 TmA^–1 

I = current

n = number of turns per unit length of solenoid

i.e. n = $\frac{N}{l}$, N = total number of turns.

4. Magnetic field due to a toroid. 

B = ${{\mu }_{o}}$n I

Where, ${{\mu }_{o}}$ = Magnetic permeability of free space,

_{${{\mu }_{o}}$} = 4$\pi $×10^–7 TmA^–1 

I = current

n = number of turns per unit length of toroid.

i.e. n = $\frac{N}{l}$, N = total number of turns.

Q.18. A horizontal wire, of length 5 cm and carrying a current of 2 A, is placed in the middle of a long solenoid at right angles to its axis. The solenoid has 1000 turns per meter and carries a steady current I. Calculate I if the force on the wire is equal to 10^–4 N (${{\mu }_{o}}$ = 4$\pi $×10^–7 Hm^–1)

Solution:

Here,

Length of the wire, l = 5 cm = 5×10^–2 m

Current in the wire, I_w = 2 A

Angle between wire and magnetic field due to solenoid,$\theta $ = 90^o

Number of turns per unit length, n = 1000 m^–1

Current through the solenoid, I_s = ?

Force experienced by wire, F_w = 10^–4 N

${{\mu }_{o}}$ = 4$\pi $×10^–7 Hm^–1

We have,

F_w = B_s I_w l_w sin$\theta $………(i)

Also, magnetic field due to solenoid, B_s = ${{\mu }_{o}}$n I_s

From equation (i),

F_w = ${{\mu }_{o}}$n I_s× I_w l_w sin$\theta $

I_s = $\frac{{{F}_{w}}}{{{\mu }_{o}}n{{I}_{w}}{{l}_{w}}sin{{90}^{o}}}$ 

I_s = $\frac{{{10}^{-4}}}{4\pi \times {{10}^{-7}}\times 1000\times 2\times 5\times {{10}^{-2}}\times 1}$ = 0.796 A

5. Magnetic field due to a current carrying straight conductor:

  B = $\frac{{{\mu }_{o}}I}{2\pi a}$

6. Force between parallel current carrying conductors:

(i) When current flows in same direction (Like current)

F₁ = F₂ = $\frac{{{\mu }_{o}}{{I}_{1}}{{I}_{2}}}{2\pi a}$

This force is attractive in nature. 

2. When current flows in opposite direction (Unlike current)

F₁ = F₂ = $\frac{{{\mu }_{o}}{{I}_{1}}{{I}_{2}}}{2\pi a}$

This force is repulsive in nature. 

Q.19. Two long parallel conductors carry respectively currents of 12A and 8A in the same direction. If the wires are 10 cm apart, find where a third parallel wire also carrying a current must be placed so that the force experienced by it will be zero.

Solution:

Here,

The current through conductor A, I₁ = 12 A 

The current through conductor B, I₂ = 8 A

Distance between them, d = 10 cm = 0.1m

Let the current through conductor C = I

For zero force,

F_AC = F_BC

Or, $\frac{{{\mu }_{o}}{{I}_{1}}I}{2\pi x}$= $\frac{{{\mu }_{o}}{{I}_{2}}I}{2\pi (0.1-x)}$

Or, 12(0.1-x) = 8x

Or, 12×0.1–12x = 8x

Or, 20x = 12 × 0.1

Or, x = $\frac{12\times 0.1}{20}$ 

Or, x = 0.06 m from first conductor.

Q.20.  What will be the resultant magnetic field at origin due to four infinite current carrying wires A, B, C, & D. Each wire carries current ( I = 2A) and is equidistance (10cm) from origin.

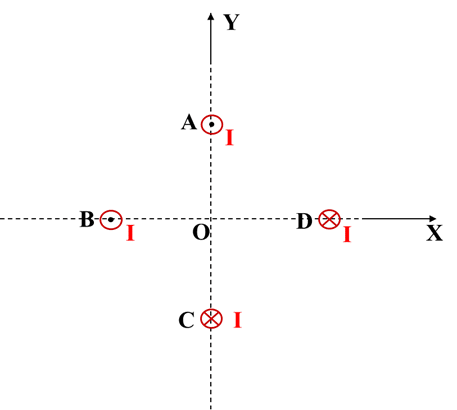
Ans: 1.13×10^–5 T

Q.21. Calculate the magnetic field at the centre of coil in the form of a square of side 4cm carrying a current of 5A.

Ans: 1.41×10^-4T

Q.22. A current of magnitude 3A enters at point B of a triangular frame of uniform wire ABC (i) Find the magnetic field at the centroid ‘O’ of the given equilateral triangle (each side of length 3cm).

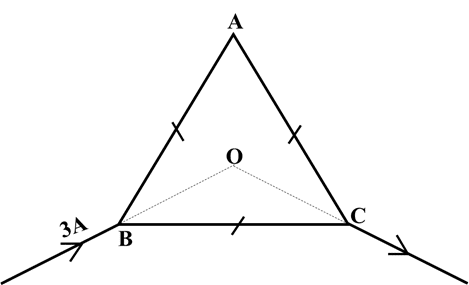
Ans: 0 T

Q.23. In the given circuit 9A current is divided into I₁ and I₂. If the radius of the circle is 10cm, (i) find the ratio of magnetic field at point O due to currents I₁ and I₂. (ii) Also find the resultant magnetic field at point O due to currents I₁ and I₂.

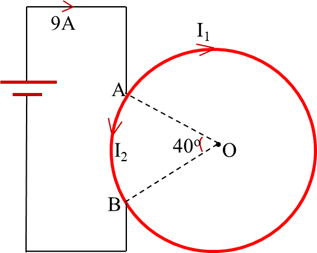
Ans: 1:1, 0T

Q.24.  A straight conductor carrying current ‘I’ is split into circular loop as shown in figure. Find the magnetic induction at the centre of circular loop. 

Ans: 0 T

Q.25.  An infinitely long straight conductor is bent into the shape as shown in figure. It carries a current of ‘I’ Amp and radius of circular loop is ‘r’. Find the magnetic induction at the centre of the circular loop.

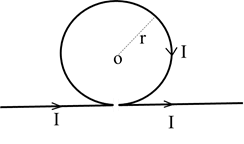
Ans:

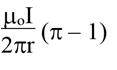
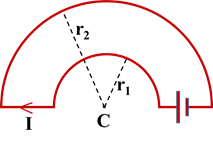
Q.26.  A wire formed by joining two semicircular wires of radii ‘r₁‘ and ‘r₂‘ carries a current ‘I’ as shown. Find the magnitude of magnetic induction at the centre ‘C’ .

Ans:

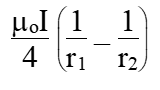
Q.27. Figure shows that a rectangular metal frame ABCD placed in a uniform magnetic field  of flux density 4.5×10^–3 T.

1.Calculate the force experienced by side AB.

2. Why side BC does not experiences force ? Explain.

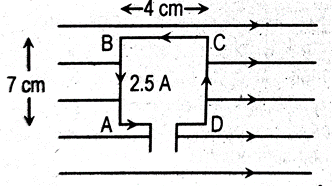
Ans: 7.875×10^–4 N

Type-5:

8. Torque on a rectangular coil suspended in uniform magnetic field.

$\tau $ = BINA cos$\theta $

Where, 

$\tau $ = Torque

B = Magnetic field

I = current in the coil

N = number of turns

A = Area of coil

$\theta $ = angle between magnetic field and coil

9. Moving coil galvanometer

At equilibrium condition, 

Deflecting / applied torque = Restoring torque

${{\tau }_{d}}$ = ${{\tau }_{R}}$

or, BINA  =  C$\theta $

where, $\theta $ = deflection in galvanometer

C = torsion constant

(i) Current sensitivity

It is defined as the deflection per unit current. 

We have, 

C. $\theta $ =  BINA

$\frac{\theta }{I}$  = $\frac{BNA}{C}$

$\therefore $ current sensitivity, S_I  = $\frac{BNA}{C}$

(ii) Voltage sensitivity

It is defined as the deflection per unit potential difference.

We have,

C.$\theta $ =  BINA

$\frac{\theta }{I}$  = $\frac{BNA}{C}$

$\frac{\theta }{IR}$  = $\frac{BNA}{CR}$

$\frac{\theta }{V}$  = $\frac{BNA}{CR}$

$\therefore $ Voltage sensitivity, S_V = $\frac{BNA}{CR}$

Q.28. The coil of a moving coil galvanometer has 50 turns and its resistance is 10$\Omega $. It is replaced by a coil having 100 turns and resistance 50$\Omega $. Find the factor by which the current and voltage sensitivities change.

Solution:

Here,

Case-1:

Number of turns, N₁ = 50 turns

Resistance of coil of galvanometer, R₁ = 10$\Omega $

Case-2:

Number of turns, N₂ = 100 turns

Resistance of coil of galvanometer, R₂ = 50$\Omega $

(i) Factor by which current sensitivity change, $\frac{{{({{S}_{I}})}_{2}}}{{{({{S}_{I}})}_{1}}}$= ?

(ii) Factor by which voltage sensitivity change, $\frac{{{({{S}_{V}})}_{2}}}{{{({{S}_{V}})}_{1}}}$= ?

For current sensitivity,

Case-1:

(S_I)₁ = ${{\left( \frac{\theta }{I} \right)}_{1}}$= $\frac{BI{{N}_{1}}A\,cos\theta }{C}$…… (i)

Case-2:

(S_I)₂ = ${{\left( \frac{\theta }{I} \right)}_{2}}$= $\frac{BI{{N}_{2}}A\,cos\theta }{C}$…… (ii)

Dividing equation (ii) by (i), we get

$\frac{{{({{S}_{I}})}_{2}}}{{{({{S}_{I}})}_{1}}}$ = $\frac{{{N}_{2}}}{{{N}_{1}}}$= $\frac{100}{50}$= 2

For voltage sensitivity,

Case-1:

(S_v)₁ = ${{\left( \frac{\theta }{V} \right)}_{1}}$= $\frac{BI{{N}_{1}}A\,cos\theta }{C{{R}_{1}}}$…… (iii)

Case-2:

(S_v)₂ = ${{\left( \frac{\theta }{V} \right)}_{2}}$= $\frac{BIN{}_{2}Acos\theta }{C{{R}_{2}}}$…… (iv)

Dividing equation (iv) by (iii), we get

$\frac{{{({{S}_{V}})}_{2}}}{{{({{S}_{V}})}_{1}}}$= $\frac{{{N}_{2}}}{{{R}_{2}}}$×$\frac{{{R}_{1}}}{{{N}_{1}}}$ 

Or, $\frac{{{({{S}_{V}})}_{2}}}{{{({{S}_{V}})}_{1}}}$= $\frac{100}{50}$×$\frac{10}{50}$

$\therefore $  $\frac{{{({{S}_{V}})}_{2}}}{{{({{S}_{V}})}_{1}}}$= $\frac{2}{5}$ 

Q.29. Two galvanometers which are otherwise identical are fitted with different coils. One has a coil of 50 turns and resistance 10$\Omega $ while the other has 500 turns and a resistance of 600$\Omega $. What is the ratio of the deflection when each is connected in turns to a cell of emf 25 V and internal resistance 50$\Omega $ ?

Solution:

Here,

Case-1:

Number of turns, N₁ = 50 turns

Resistance of coil of galvanometer, R₁ = 10$\Omega $

Case-2:

Number of turns, N₂ = 500 turns

Resistance of coil of galvanometer, R₂ = 600$\Omega $

Ratio of deflection, $\frac{{{\theta }_{1}}}{{{\theta }_{2}}}$= ?

Emf, E = 25 V

Internal resistance of the cell, r = 50$\Omega $

Using circuit formula, E = I (R + r)

Case-1,

E = I₁ (R₁ + r)

Or, I₁ = $\frac{E}{{{R}_{1}}+r}$ 

Or, I₁ = $\frac{25}{10+50}$

Or, I₁ = $\frac{5}{12}$A

Case-2,

E = I₂ (R₂ + r)

Or, I₂ = $\frac{E}{{{R}_{2}}+r}$

Or, I₂ = $\frac{25}{600+50}$

Or, I₂ = $\frac{1}{26}$A

Now, we know that

Restoring torque = Applied (deflecting) torque

From case-1, C${{\theta }_{1}}$ = B I₁N₁A cos$\theta $ ………..(i)

From case-2, C${{\theta }_{2}}$ = B I₂N₂A cos$\theta $ ………..(ii)

Dividing equation (i) by (ii)

$\frac{{{\theta }_{1}}}{{{\theta }_{2}}}$= $\frac{{{I}_{1}}{{N}_{1}}}{{{I}_{2}}{{N}_{2}}}$ 

Or,   $\frac{{{\theta }_{1}}}{{{\theta }_{2}}}$= $\frac{5}{12}$×26×$\frac{50}{500}$

$\therefore $   $\frac{{{\theta }_{1}}}{{{\theta }_{2}}}$= $\frac{13}{12}$

Type-6:

10. Hall’s Effect

(i) Hall voltage,

V_H  = $\frac{{{B}_{Z}}{{I}_{X}}}{net}$ [or, simply V_H  = $\frac{BI}{net}$ ]

Where,

V_H  = Hall voltage

B_Z = Magnetic field (applied along Z-axis)

I_X = Current (flowing along X-axis)

n = Number of electrons per unit volume.

t = thickness along the magnetic field.

(ii) Hall coefficient

R_H = – $\frac{1}{ne}$is constant and known as Hall coefficient.

Q.30. A flat silver strip of width 1.5 cm and thickness 1.5 mm carries a current of 150 A. A magnetic field of 2 T is applied perpendicular to the flat face of the strip. The emf developed across the width of the strip is measured to be 17.9 $\mu $V. Calculate the free electron density in the silver.

 Solution:

Here,

Width, b = 1.5 cm = 1.5 ×10^–2 m

Thickness, t = 1.5 mm = 1.5 ×10^–3 m

Current, I = 150 A

Magnetic field, B = 2 T

Hall voltage, V_H = 17.9 $\mu $V = 17.9×10^–6 V

Free electron density, n = ?

We know,

Hall voltage, V_H  =$\frac{{{B}_{Z}}I{}_{X}}{net}$

Or, n = $\frac{{{B}_{Z}}{{I}_{X}}}{{{V}_{H}}et}$

Or, n = $\frac{2\times 150}{17.9\times {{10}^{-6}}\times 1.6\times {{10}^{-19}}\times 1.5\times {{10}^{-3}}}$

$\therefore $ Free electron density, n = 6.98×10²⁸ m^–3

Q.31. A slab of copper 2 mm thick and 1.50 cm wide, is placed in a uniform magnetic field of flux density 0.40 T, so that the maximum passes through the slab. When a current of 75 A flows through it, a potential difference of 0.81 $\mu $V is developed between the edges of the slab. Find the concentration of the mobile electrons in copper.

Solution:

Here,

Thickness, t = 2 mm = 2 ×10^–3 m

Width, b = 1.5 cm = 1.5 ×10^–2 m

Magnetic field, B = 0.4 T

Current, I = 75 A

Hall voltage, V_H = 0.81 $\mu $V = 0.81×10^–6 V

Concentration of mobile electrons, n = ?

We know,

Hall voltage, V_H  = $\frac{{{B}_{Z}}I{}_{X}}{net}$

Or, n = $\frac{{{B}_{Z}}{{I}_{X}}}{{{V}_{H}}et}$

Or, n = $\frac{0.4\times 75}{0.81\times {{10}^{-6}}\times 1.6\times {{10}^{-19}}\times 2\times {{10}^{-3}}}$

$\therefore $ Concentration of mobile electrons, n = 1.16×10²⁹ m^–3

Q.32. A slice of indium antimonide is 2.5 mm thick and carries a current of 150 mA. A magnetic field of flux density 0.5 T, correctly applied, produces a maximum Hall Voltage of 8.75 mV between the edges of the slice. Calculate the number of free charge carriers per unit volume assuming that each has a charge of 1.6×10^–19 C. 

Solution:

Here,

Thickness, t = 2.5 mm = 2.5 ×10^–3 m

Current, I = 150 mA = 150 ×10^–3 A

Magnetic field, B = 0.5 T

Hall voltage, V_H = 8.75 mV = 8.75×10^–3 V

Number of free electrons per unit volume, n = ? 

Charge of electron, e = 1.6×10^–19 C

We know,

Hall voltage, V_H  = $\frac{{{B}_{Z}}I{}_{X}}{net}$

Or, n = $\frac{{{B}_{Z}}{{I}_{X}}}{{{V}_{H}}et}$

Or, n = $\frac{0.5\times 150\times {{10}^{-3}}}{8.75\times {{10}^{-3}}\times 1.6\times {{10}^{-19}}\times 2.5\times {{10}^{-3}}}$

$\therefore $ Number of free electrons per unit volume, n = 2.143×10²² m^–3

Also Read: Magnetic Effect of Current Notes Class 12