Heating effect of current:
When current flows through a conductor, heat develops in it. This effect of current is known as heating effect of current.
When current flows through a conductor, the free electrons of the conductor come in motion and collision takes place between them. Due to the collision moving electrons lose their kinetic energy and some part of their kinetic energy is converted into heat energy.
Joule’s law of heating:
Let us consider a conductor of resistance (R). Let an amount of current (I) is passed through the conductor for time ‘t’. According to Joule’s law of heating, the heat developed in the conductor is
(i) directly proportional to square of magnitude of current flowing through the conductor.
i.e. H $\propto $ I2 ………….(i)
(ii) directly proportional to resistance of conductor.
i.e. H $\propto $ R …………..(ii)
(iii) directly proportional to the time for which current is passed through the conductor.
i.e. H $\propto $ t …………..(iii)
On combining (i), (ii) and (iii) we get,
H $\propto $ I2Rt
or, H = k I2Rt
Where ‘k’ is proportionality constant and its value is 1 in S.I.
H = I2Rt
The above result also can be written as
H = $\frac{{{I}^{2}}Rt}{J}$, where ‘J’ is Joule’s equivalent and its value is 4.2 joules/calorie.
Derivation for the expression of heat developed in a wire.
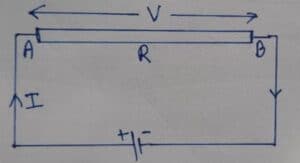
Let us consider a wire AB of resistance R in a circuit as shown in Fig. Let (I) be the steady current passing through it.
In time ‘t’ the total charge ‘q’ passing through B to A is given by
I = $\frac{q}{t}$
or, q = I.t
Let the potential difference between A and B be (V). Then,
V = IR
The work done to transfer the charge (q) from B to A is given by,
W = qV
From equations (i), (ii) and (iii) we get,
W = I t. I R
Or, W = I2 R t
It the wire is a passive resistor, all the electrical energy is converted into the heat energy, H.
So, W = H and we have,
H = I2Rt Joule
This is the expression for heat developed in a wire of resistance R.
Experimental verification of Joule’s law of heating:

The experimental setup for verification of Joule’s law of heating is shown in figure above. It consists of a calorimeter with stirrer filled with water about two third of its volume. A heating coil is placed well inside water. The heating coil is connected with a battery through a key, a rheostat (variable resistance) and an ammeter as shown in figure. The variable resistance is used to change the value of current and ammeter is used to measure the value of current.
(i) Verification of first law (i.e. H $\propto $ I2)
Let ‘m’ be the mass of water in the calorimeter of water equivalent ‘W’, specific heat capacity of water is ‘S’.
Now, I1 amount of current is passed through the heating coil of resistance R for time ‘t’. It is found that the temperature of water and calorimeter increases from $\theta $1 to $\theta $2. Now heat developed is
H1 = w($\theta $2 – $\theta $1) + ms($\theta $2 – $\theta $1)
Let H2, H3 and H4 be the heat developed when different amounts of current I2, I3,I4…………..are passed through the same heating coil for some time, it is found that
$\frac{{{H}_{1}}}{{{I}_{1}}^{2}}$= $\frac{{{H}_{2}}}{{{I}_{2}}^{2}}$= $\frac{{{H}_{3}}}{{{I}_{3}}^{2}}$= $\frac{{{H}_{4}}}{{{I}_{4}}^{2}}$ …
Now, we can write,
$\frac{H}{{{I}^{2}}}$ = constant
It gives H $\propto $ I2
If we plot a graph for different value of H and I2, a straight line passing through the origin will be obtained.
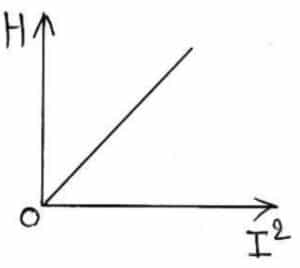
It verifies first law.
(ii) Verification of second law (i.e. H $\propto $ t)
To verify this law, heating coils of different lengths are taken. Let R1, R2, R3, R4……..be the resistances of different heating coils. If same amount of current is passed through the different heating coils of resistance R1, R2, R3, R4 for same time the corresponding heat developed is found to be H1, H2, H3, H4……..respectively. Now, it is found that
$\frac{{{H}_{1}}}{{{R}_{1}}}$= $\frac{{{H}_{2}}}{{{R}_{2}}}$= $\frac{{{H}_{3}}}{{{R}_{3}}}$= $\frac{{{H}_{4}}}{{{R}_{4}}}$ …
Now, we can write,
$\frac{H}{R}$= constant
It gives H $\propto $ R
If we plot a graph for different value of H and R, a straight line passing through the origin will be obtained.
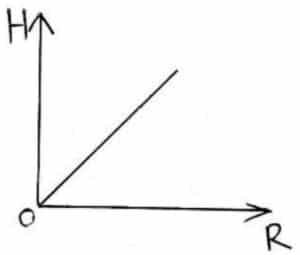
It verifies second law.
(iii) Verification of third law (i.e. H $\propto $ t)
To verify this law, same amount of current is passed through the same heating coil for different time t1, t2, t3, t4………..the corresponding heat developed are H1, H2, H3, H4……….respectively. It is found that
$\frac{{{H}_{1}}}{{{t}_{1}}}$= $\frac{{{H}_{2}}}{{{t}_{2}}}$= $\frac{{{H}_{3}}}{{{t}_{3}}}$= $\frac{{{H}_{4}}}{{{t}_{4}}}$………………..
Now, we can write,
$\frac{H}{t}$= constant
It gives H $\propto $ t
If we plot a graph for different value of H and t, a straight line passing through the origin will be obtained.
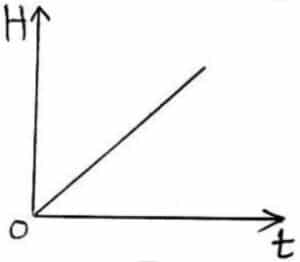
It verifies third law.
Electric power:
This is defined as the electrical energy per unit time.
Mathematically,
Electric power, P = $\frac{H}{t}$ = $\frac{{{I}^{2}}Rt}{t}$
P = I2R ………(i)
P = I×IR
P = IV ………(ii) Since, V = IR
P = $\frac{V}{R}$ × V Since, I = $\frac{V}{R}$
P = $\frac{{{V}^{2}}}{R}$ …………..(iii)
From (i), (ii) and (iii)
P = I2R = IV = $\frac{{{V}^{2}}}{R}$
One unit or 1 kilowatt-hour of electrical energy:
Electric power is defined as the electrical energy per unit time.
Electric power, P = $\frac{Electric\text{ }energy}{time}$
Electric energy = P×t
If P =1 KW and t = 1 hour
Then,
Electric energy = 1 KW × 1 hr
= 1 KWhr
= 1 unit
Electric energy consumed is said to be one unit if an electric device of 1KW power is used for 1 hour.
Also Read: EMF of a Cell Class 12 Notes