Kinematics Class 11 Physics | Notes

Kinematics:

The branch of physics which deals with the study of motion as the function of time is known as kinematics. It does not give any information about force that causes it to move.

Rest:

An object is said to be in rest if it does not changes its position with respect to a reference point.

Motion:

An object is said to be in motion if it changes its position with respect to a reference point.

Motion in straight line

Distance:

The total length of actual path moved by an object from its initial position to final position is known as distance. It is a scalar quantity.

The distance of a moving body can be never be zero. Its unit is metre (m).

Displacement:

The shortest distance between any two points in specified direction. (i.e. initial to final) is known as displacement. It is vector quantity and denoted by ($\overrightarrow{S}$)

The displacement of a moving body may be zero. Its unit is metre (m).

Note: The ratio of distance to magnitude of displacement is greater than or equal to 1

Q. An object moves 3.5 times around a circular path of radius 100m. Calculate its total distance and total displacement. 

Solution:

Given,

Radius, r = 100 m

Distance, S = 2$\pi $r × n = 2×$\frac{\text{22}}{\text{7}}$×100×3.5 = 2200m

Displacement, ($\overrightarrow{S}$) = 2r = 2×100= 200m

Q. A car is moving on a circular track of radius 70m. Find the distance and displacement made when the car reaches to opposite end of the track.

Solution:

Here,

Radius, r = 70m.

Distance, S = $\frac{\text{2 }\!\!\pi\!\!\text{ }\text{r}}{\text{2}}$

= $\frac{\text{22}}{\text{7}}$×70

= 220m

Displacement, ($\overrightarrow{S}$)= 2r

= 2×70

= 140m

Speed:

It is defined as the rate of change of distance with respect to time.

Mathematically, speed= $\frac{\text{distance(s)}}{\text{time(t)}}$

Its unit is ms^–1. It is a scalar quantity.

Types of Speed:

(i) Average speed:

It is defined as the ratio of total distance covered to the total time taken.

Mathematically, average speed = $\frac{\text{total distance}}{\text{total time}}$

Avg. speed = $\frac{\text{total distance}}{\text{total time}}$ = $\frac{{{\text{S}}_{\text{1}}}\text{+}{{\text{S}}_{\text{2}}}\text{+}{{\text{S}}_{\text{3}}}}{{{\text{t}}_{\text{1}}}\text{+}{{\text{t}}_{\text{2}}}\text{+}{{\text{t}}_{\text{3}}}}$= $\frac{\sum S}{\sum t}$

(ii) Uniform speed:

The speed of an object is said to be uniform if it covers equal distances in equal interval of time. 

                             

(iii) Non-uniform speed:

The speed of an object is said to be non-uniform if it covers unequal distances in equal interval of time.

(iv) Instantaneous speed:

The speed of an object calculated for very small interval of time is called instantaneous speed.

Mathematically, V_ins=  $\underset{\Delta t\to 0}{\mathop{\lim }}\,\text{ }\frac{\Delta s}{\Delta t}$

Velocity:

The rate of change of displacement with respect to time is known as velocity.

Mathematically, Velocity = $\frac{\text{displacement}}{\text{time}}$

It’s unit is ms^–1. It is a vector quantity.

Types of velocity:

(i) Average velocity:

It is defined as the ratio of total displacement covered to total time taken.

Mathematically, average velocity = $\frac{\text{total displacement}}{\text{total time}}$                                                        

(ii) Uniform velocity:

The velocity of an object is said to be uniform if it covers equal displacements in equal interval of time.

(iii) Non-uniform velocity:

The velocity of an object is said to be non-uniform if it covers unequal displacements in equal interval of time.

(iv) Instantaneous velocity:

The velocity of an object calculated for very small interval of time is called instantaneous velocity.

Mathematically, $\overrightarrow{{{V}_{ins}}}$= $\underset{\Delta t\to 0}{\mathop{\lim }}\,\text{ }\frac{\overrightarrow{\Delta s}}{\Delta t}$=$\frac{\overrightarrow{ds}}{dt}$

Note: (i) If time is equally divided then the average speed is V =  $\frac{{{\text{v}}_{\text{1}}}\text{+}{{\text{v}}_{\text{2}}}}{\text{2}}$

         (ii) If distance is equally divided, then the average speed is     V =  $\frac{\text{2}{{\text{v}}_{\text{1}}}{{\text{v}}_{\text{2}}}}{{{\text{v}}_{\text{1}}}\text{+}{{\text{v}}_{\text{2}}}}$

         (iii) For uniform motion i.e. constant velocity, $\overrightarrow{{{V}_{avg}}}$=  $\overrightarrow{{{V}_{ins}}}$

Facts about uniform velocity:

(i)         The object always moves in a straight line and in the same direction.

(ii)        The magnitude of velocity is equal to speed.

(iii)       The average velocity is equal to instantaneous velocity.

(iv)       Since velocity is constant, acceleration is zero and hence net force (resultant force) is also zero.

Acceleration and retardation (or deceleration):

The rate of change of velocity with respect to time is known as acceleration. It is denoted by ‘a’ and given by

                                     a = $\frac{v-u}{t}$    i.e. v = u+at

It is a vector quantity retardation. The negative value of acceleration is called retardation (or deceleration).

For uniform velocity, acceleration is zero.

Equations related to uniform acceleration.

1.      v = u+at

2.      S = ut + $\frac{1}{2}$at²

3.      V² = u² + 2as

Types of acceleration

(a) Average acceleration,

$\overrightarrow{{{a}_{avg}}}$= $\frac{\overrightarrow{\Delta v}}{\Delta t}$

(b) Instantaneous acceleration,

$\overrightarrow{{{a}_{ins}}}$= $\underset{\Delta t\to 0}{\mathop{\lim }}\,\text{ }\frac{\overrightarrow{\Delta v}}{\Delta t}$=$\frac{\overrightarrow{dv}}{dt}$

Graphical treatment:

(i)         Displacement- time graph for uniform motion

(i.e. velocity, V = constant and acceleration, a = 0)

Slope = $\frac{BC}{AC}$ = velocity

(ii)        Displacement- time graph for non-uniform motion

Slope at P = $\frac{BC}{AC}$= Velocity at point P

(iii)       Velocity – time graph for uniform motion

(i.e. velocity, V = constant and acceleration, a = 0)

(iv) Velocity – time graph for constant acceleration (for u = 0)

(v) Velocity – time graph for constant acceleration (for u > 0)

(vi) Velocity – time graph for non-uniform acceleration.

Slope at P = $\frac{BC}{AC}$ = acceleration at point P

Displacement-time graph (s-t graph):

 Fig: Displacement-time graph for uniform motion

Let us consider a body initially at S_o is moving with constant velocity for time ‘t’ where it covers distance ‘S’. Let this motion is represented by line AB in a s-t graph.

Draw BM perpendicular to t-axis and AN perpendicular to BM.

OA = MN = S_o

OM = AN = t

BN = BM – MN = S – S_o

We have,

Slope of S-t graph  = Slope of line AB

=  $\frac{BN}{AN}$

= $\frac{S-{{S}_{o}}}{t}$ = velocity         

$\therefore $  Slope of S-t graph = Velocity of a body

Physical significance of s-t graph

• The slope of (s-t) graph gives velocity   i.e.$\overrightarrow{V}$= $\frac{\overrightarrow{\Delta s}}{\Delta t}$
• It gives position of a body at any instant.
• It gives distance covered by a body in any interval of time.  

(i) Derivation of   S = S_o + vt for a body moving with constant velocity by graphical method.

Let us consider a body initially at S_o is moving with constant velocity for time ‘t’ where it covers distance ‘S’. Let this motion is represented by line AB in a s-t graph.

Draw BM perpendicular to t-axis and AN perpendicular to BM.

OA = MN = S_o

OM = AN = t

BN = BM – MN = S – S_o

We have, Slope of S-t graph = velocity

Slope of line AB = V

  $\frac{BN}{AN}$ = V

$\frac{S-{{S}_{o}}}{t}$ = v

$\therefore $ S = S_o + vt ……….is the required expression for displacement.

Velocity-time graph (v-t graph):

Let us consider a body moving initially with velocity ‘u’ is accelerated for time ‘t’ and velocity increases to ‘v’. Let this motion is represented by line AB in v-t graph.

Draw perpendicular BM to t-axis AN perpendicular to BM.

OA = MN = u

OM = AN = t

BN = BM – MN = v -u

We have,

Slope of v-t graph = slope of line AB

= $\frac{BN}{AN}$  =  $\frac{v-u}{t}$ = a

$\therefore $ Slope of v-t graph  = acceleration

Also, Area of v-t graph with t- axis = Area of trapezium OABM

= Area of rectangle OANM + Area of triangle ABN

= OA× OM + $\frac{1}{2}$ AN ×BN

=  ut + $\frac{1}{2}$ t × at =  displacement (S)

$\therefore $ Area of v-t graph with t- axis = displacement (S)

Physical significance of v-t graph are

• The slope of (v – t) graph gives acceleration   i.e.$\overrightarrow{a}$= $\frac{\overrightarrow{\Delta v}}{\Delta t}$
• The area under (v – t) graph with time – axis gives displacement .
• It gives velocity at any instant of time.

Kinematical equations by graphical method:

(i) Derive v = u + at for a body with constant acceleration by graphical method.

Let us consider a body moving initially with velocity ‘u’ is accelerated for time ‘t’ and velocity increases to ‘v’. Let this motion is represented by line AB in v-t graph.

Draw perpendicular BM to t-axis and AN perpendicular to BM.

OA = MN = u

OM = AN = t

BN = BM – MN = v -u

We know,

Slope of v-t graph = acceleration

i.e. slope of line AB = a

Or,    $\frac{BN}{AN}$ = a

Or,   $\frac{v-u}{t}$ = a

$\therefore $ v = u + at  ………This is the required expression.

(ii) Derivation of S = ut + $\frac{\text{1}}{\text{2}}$ at² for a uniformly accelerating body by graphical method.

Let us consider a body moving initially with velocity ‘u’ is accelerated for time ‘t’ and velocity increases to ‘v’. Let this motion is represented by line AB in v-t graph.

Draw perpendicular BM to t-axis AN perpendicular to BM.

OA = MN = u

OM = AN = t

BN = BM – MN = v -u

We know,

Slope of v-t graph = acceleration

i.e. slope of line AB = a

Or,    $\frac{BN}{AN}$ = a

Or, BN = at

Now, Area of v-t graph with t- axis = distance

Or, Area of trapezium OABM = S

Or, Area of rectangle OANM + Area of triangle ABN = S

Or, OA× OM + $\frac{1}{2}$ AN ×BN = S

Or, ut + $\frac{1}{2}$ t × at = S

$\therefore $ S = ut + $\frac{\text{1}}{\text{2}}$ at²………This is the required expression.

(iii)  Derivation of  v² = u² + 2as for a uniformly accelerating body by graphical method.

Let us consider a body moving initially with velocity ‘u’ is accelerated for time ‘t’ and velocity increases to ‘v’. Let this motion is represented by line AB in v-t graph.

Draw perpendicular BM to t-axis AN perpendicular to BM.

OA = MN = u

OM = AN = t

BN = BM – MN = v – u

We know,

Slope of v-t graph = acceleration

i.e, slope of line AB = a

Or, $\frac{BN}{AN}$ = a

Or, AN = $\frac{v-u}{a}$ ………………. (i)

Now, Area of v-t graph with t- axis = distance

i.e, Area of trapezium OABM = S

Or, $\frac{1}{2}$ (OA + BM) × AN = S

Or, $\frac{1}{2}$ ( u + v)  $\frac{v-u}{a}$ = S

Or, $\frac{{{v}^{2}}-{{u}^{2}}}{2a}$ = S                 

Or, v² – u² = 2as

$\therefore $ v² = u² + 2as ………..This is the required expression.

Distance covered by a body in n^th second ( S_n^th formula):

The distance covered by a body in the interval of ‘n’ sec and (n-1) sec is called S_n^th formula.

It is given by S_n^th = S_n – S_n-1

i.e, S_n^th  = u + $\frac{a}{2}$ (2n – 1)

Derivation:

Let us consider a body moving initially with velocity ‘u’ is accelerated to distances S_n and S_n-1 in ‘n’ sec and (n-1) sec respectively.

As we know,    S = ut + $\frac{1}{2}$ at²

So,    S_n = u × n + $\frac{1}{2}$ an² ……………..(i)

and   S_n-1 = u(n-1) + $\frac{1}{2}$ a(n-1)² ……………….(ii)

Now, distance covered in n^th second = S_n – S_n-1

Or,       S_n^th  ₌ un + $\frac{1}{2}$ an² – [u(n-1) + $\frac{1}{2}$ a(n-1)²)]

Or,       S_n^th = un + $\frac{1}{2}$ an² – [un-u + $\frac{1}{2}$ a(n²– 2n+1)]

Or,       S_n^th = un + $\frac{1}{2}$ an² – [un – u ₊ $\frac{1}{2}$ an² – an +$\frac{1}{2}$ a]

Or,       S_n^th = un + $\frac{1}{2}$ an² – un + u – $\frac{1}{2}$ an² + an – $\frac{1}{2}$ a

Or,      S_n^th = u + a( n- $\frac{1}{2}$ )

$\therefore $ S_n^th = u + $\frac{\text{a}}{\text{2}}$ (2n – 1)…………………is the required expression.

Projectile

Projectile: 

An object which is thrown in space and falls under the action of gravity alone is known as projectile. We neglect air resistance during the projectile motion. The path followed by projectile is known as trajectory.

Examples of projectile:

i. A stone thrown into space.

ii. A ball thrown towards a player in a playground. 

iii. A bomb dropped from an airplane.

Assumptions for the study of projectile motion 

1. The acceleration along y–axis is only considered, i.e. the projected object falls under the action of gravity alone.

2. The acceleration along x–axis is zero (a_x = 0). The horizontal velocity does not change at all throughout the projectile motion, i.e. u_x = V_x 

3. Air resistance is neglected.

Case I: When an object is projected making an angle ‘$\theta $’ with the horizontal.

Let us consider an object projected from ground with an initial speed ‘u’ making an angle ‘$\theta $’ with horizontal (ground) as shown in figure.

Resolving the initial velocity ‘u’ into its rectangular components, we get, 

u_x = u cos$\theta $ and u_y = u sin$\theta $ along horizontal and vertical direction respectively.

1. Path of the projectile:

Let S_x = x and S_y = y be the components of displacement along horizontal and vertical direction respectively at any point.

We know, S = ut + $\frac{1}{2}$at² …………(i)

Taking horizontal component, equation (i) becomes,

 S_x = u_xt + $\frac{1}{2}$a_xt²  

Or, x = u cos$\theta $.t    $\because $ a_x= 0

Or, t = $\frac{x}{u\cos \theta }$………….(ii)

Taking vertical component, equation (i) becomes,

 S_y = u_yt + $\frac{1}{2}$a_yt²  

Or, y = u sin$\theta $$\frac{x}{u\cos \theta }$ + $\frac{1}{2}$(–g) ${{\left( \frac{x}{u\cos \theta } \right)}^{2}}$

Or, y = tan$\theta $.x – $\frac{g}{2{{u}^{2}}{{\cos }^{2}}\theta }$x²

This equation is of the parabolic form y = ax + bx²,

where, a = tan$\theta $ and b = $\frac{-g}{2{{u}^{2}}{{\cos }^{2}}\theta }$

2. Maximum Height (H_max):

It is the maximum vertical displacement attained by the projectile.

We know, v² = u² + 2as ….(iii)

Taking vertical component, equation (iii) becomes,

v_y² = u_y² + 2 a_y s_y

For maximum height, s_y = H_max and v_y = 0

$\therefore $ 0 = u²sin² $\theta $ + 2 (-g) H_max

Or, 2 g H_max = u²sin² $\theta $

$\therefore $ H_max = $\frac{{{u}^{2}}si{{n}^{2}}\theta }{2g}$ 

This is the required expression for maximum height.

3. Time of flight (T):

It is the total time spent by projectile in air.

We know, S = ut + $\frac{1}{2}$at² …………(iv)

Taking vertical component, equation (iv) becomes,

 S_y = u_yt + $\frac{1}{2}$a_yt²  

For time of flight (total time), t = T and S_y = 0

Or, 0 = u sin$\theta $. T + $\frac{1}{2}$(–g) T²

Or, $\frac{1}{2}$g T² = u sin$\theta $. T

$\therefore $T = $\frac{2u\sin \theta }{g}$

This is the required expression for time of flight.

Time to reach the greatest height / time of ascend (t_asc) / time of descend (t_des):

T_1/2 = t_asc = t_des =  $\frac{T}{2}$= $\frac{u\sin \theta }{g}$

4. Horizontal Range (R):

It is the total horizontal distance covered by the projectile.

We know, S = ut + $\frac{1}{2}$at² …………(v)

Taking horizontal component, equation (v) becomes,

Or, S_x = u_xt + a_xt²  

Or, S_x = u cos$\theta $. t $\because $ a_x = 0

For horizontal range (total horizontal displacement), S_x = R and t = T, then 

R = u cos$\theta $.T

Or, R = u cos$\theta $.$\frac{2u\sin \theta }{g}$

 $\therefore $ R = $\frac{{{u}^{2}}\sin 2\theta }{g}$

This is the required expression for horizontal range.

Condition for maximum horizontal range (R_max):

We have, R = $\frac{{{u}^{2}}\sin 2\theta }{g}$

For maximum value of R, $\operatorname{sin}2\theta $ must be maximum.

i.e. $\operatorname{sin}2\theta $ = 1

Or, $\operatorname{sin}2\theta $ = Sin90^o

$\therefore $ $\theta $ = 45^o

The horizontal range is maximum for$\theta $ = 45^o.

5. Velocity of the projectile at any instant:

Let $\overrightarrow{V}$ be the velocity of the projectile at any instant. Let ‘V_x’ and ‘V_y’ be the components of velocity $\overrightarrow{V}$along x-axis and y-axis respectively and ‘$\alpha $’ be the angle made by the velocity with the horizontal.

We have V = u + at   ……. (vi)

Taking horizontal component, equation (vi) becomes,

V_x = u_x + a_xt  

Or, V_x = ucos$\theta $  {$\because $ a_x = 0} 

Similarly taking vertical component, equation (vi) becomes,

V_y = u_y + a_yt  

Or, V_y = usin$\theta $ – gt 

Now, magnitude of velocity 

V = $\sqrt{{{V}_{x}}^{2}+{{V}_{y}}^{2}}$= $\sqrt{{{u}^{2}}{{\cos }^{2}}\theta +{{\left( u\sin \theta -gt \right)}^{2}}}$

Or, V =$\sqrt{{{u}^{2}}{{\cos }^{2}}\theta +{{\left( u\sin \theta -gt \right)}^{2}}}$

and direction, $\tan \alpha $= $\frac{{{V}_{y}}}{{{V}_{x}}}$

Or, $\alpha $= tan ^–1 $\left( \frac{usin~\theta gt}{u\cos \theta } \right)$

For the velocity with which the projectile hits the ground, we replace the time ‘t’ by time of flight ‘T’ and angle ($\alpha $) by the striking angle ($\beta $)  then magnitude and direction become

Magnitude, V =$\sqrt{{{u}^{2}}{{\cos }^{2}}\theta +{{\left( u\sin \theta -gT \right)}^{2}}}$

and direction, $\beta $= tan^-1 $\left( \frac{usin~\theta gT}{u\cos \theta } \right)$

6. Two angles of projection for same horizontal range:

For the angle of projection ‘$\theta $’, the horizontal range is given by,

R₁ = $\frac{{{u}^{2}}\sin 2\theta }{g}$

Again, for the angle of projection (90 –$\theta $), the horizontal range is given by

R₂ = $\frac{{{u}^{2}}\sin 2(90-\theta )}{g}$  

=  $\frac{{{u}^{2}}\sin (180-2\theta )}{g}$

=  $\frac{{{u}^{2}}\sin 2\theta }{g}$

From above equations

R₁ = R₂

Hence, two angles of projection for the same horizontal range are $\theta $ and (90 –$\theta $ ).

Case II: When an object is projected horizontally from height (h) above the ground.

Let us consider an object projected horizontally from a height ‘h’ above the ground with initial velocity ‘u’. Here angle made by initial velocity with horizontal is zero (i.e. $\theta $= 0). In projectile motion, vertical velocity changes continuously but the horizontal velocity remains constant throughout the motion because the acceleration due to gravity doesn’t act in horizontal direction. Let ‘V_x’ and ‘V_y’ be the rectangular components of velocity ‘V’ after time ‘t’, u_y = usin0^o = 0.

1. Path of the projectile: 

Let S_x = x and S_y = y be two rectangular components of displacement along horizontal and vertical direction respectively at any point.

We know, S = ut + $\frac{1}{2}$at² …………(i)

Taking horizontal component, equation (i) becomes,

 S_x = u_xt + $\frac{1}{2}$a_xt²  

Or, x = u cos$\theta $.t    {$\because $ a_x = 0}

Or, x = u cos0^o.t     {$\because $$\theta $  = 0}

Or, t = $\frac{x}{u}$………….(ii)

Taking vertical component, equation (i) becomes,

 S_y = u_yt + $\frac{1}{2}$a_yt²  

Or, y = u sin$\theta $.t + $\frac{1}{2}$.g ^{${{\left( \frac{x}{u} \right)}^{2}}$}

Or, y = u sin0^o.t +$\frac{g}{2{{u}^{2}}}$x²

Or, y = $\frac{g}{2{{u}^{2}}}$x²

This equation is of the parabolic form y = ax²,

where, a = $\frac{g}{2{{u}^{2}}}$

2. Time of flight / time to reach the ground (T):

The total time of a projectile spent in air is known as time of flight. When the projectile reaches the ground.

We know, S = ut + $\frac{1}{2}$at² …………(iii)

Taking vertical component, equation (iii) becomes,

 S_y = u_yt + $\frac{1}{2}$a_yt²  

For total time, S_y = h and t = T

Or, h = u sin0^o.t +$\frac{1}{2}$g T²

Or, h = $\frac{1}{2}$g T² 

This is the required expression for height. 

From above equation

T² = $\frac{2h}{g}$

$\therefore $T = $\sqrt{\frac{2h}{g}}$

This is required expression for time of flight.

3. Horizontal Range (R):

We know, S = ut + $\frac{1}{2}$at² …………(iv)

Taking horizontal component, equation (iv) becomes,

 S_x = u_xt + $\frac{1}{2}$a_xt² 

S_x = u_xt {$\because $ a_x = 0}

For horizontal range (total horizontal displacement) S_x = R and t = T

Or, R = u cos0^o.T     {$\because $$\theta $  = 0}

Or, R = u  $\sqrt{\frac{2h}{g}}$

This is the required expression for horizontal range.

4. Velocity with which the projectile hits the ground.

Let $\overrightarrow{V}$ be the velocity of the projectile at any instant. Let ‘V_x’ and ‘V_y’ be the rectangular components of velocity $\overrightarrow{V}$along x-axis and y-axis respectively and ‘$\alpha $’ be the angle made by the velocity with the horizontal.

We have, V = u + at  …….  (v)

Taking horizontal component, equation (v) becomes,

V_x = u_x + a_xt  

Or, V_x = ucos$\theta $  {$\because $ a_x = 0}

 Or, V_x = ucos0^o = u 

Similarly taking vertical component, equation (v) becomes,

V_y = u_y + a_yt  

Or, V_y = usin$\theta $ + gt 

Or, V_y = gt {$\because $$\theta $= 0^o}

Now, magnitude of velocity 

V = $\sqrt{{{V}_{x}}^{2}+{{V}_{y}}^{2}}$= $\sqrt{{{u}^{2}}+{{g}^{2}}{{t}^{2}}}$

Or, V =  $\sqrt{{{u}^{2}}+{{g}^{2}}{{t}^{2}}}$

And direction, $\tan \alpha $= $\frac{{{V}_{y}}}{{{V}_{x}}}$

Or, $\alpha $= tan ^–1 $\left( \frac{gt}{u} \right)$

For the velocity with which the projectile hits the ground, we replace the time ‘t’ by time of flight ‘T’ and angle ($\alpha $) by the striking angle ($\beta $) then magnitude and direction becomes

Magnitude, V =$\sqrt{{{u}^{2}}+{{g}^{2}}{{T}^{2}}}$

And direction, $\beta $= tan ^–1 $\left( \frac{gT}{u} \right)$

Crossing of River:

Let, width of river = AB

Velocity of flow of river = V_R

Velocity of swimmer in still water = V_S 

1. For shortest route: 

(a) Direction:

Sin$\theta $ = $\frac{p}{h}$= ,

$\theta $ = sin^{–1$\left( \frac{{{V}_{R}}}{{{V}_{S}}} \right)$}

(b) Velocity along AB, V_AB = Vs cos$\theta $

(c) Time to cross the river (t) = $\frac{AB}{Vscos\theta }$

2. For least time to cross the river:

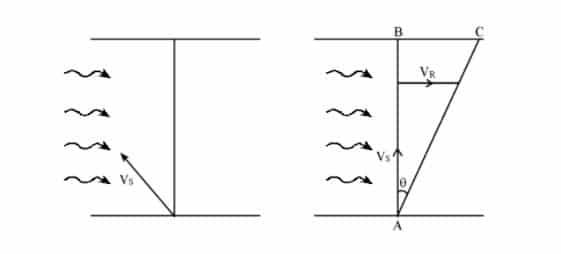
We have, 

Time to cross the river, t = $\frac{AB}{{{V}_{s}}cos\theta }$

For t_min , cos$\theta $ = max^m 

i.e. cos$\theta $ = 1

Or, cos$\theta $ =  cos0^o

Or, $\theta $ = 0^o

Then, t_min = $\frac{AB}{{{V}_{S}}}$

From fig (ii), 

Tan$\theta $ = $\frac{{{V}_{R}}}{{{V}_{s}}}$= $\frac{BC}{AB}$

Distance apart from opposite end

BC = $\frac{{{V}_{R}}}{{{V}_{s}}}$AB

$\therefore $Distance apart from the opposite end (BC) = $\frac{{{V}_{R}}}{{{V}_{s}}}$× width of river {OR, BC Tan$\theta $ × width of river} 

When a swimmer is swimming in river (Downstream or Upstream):

Let V_S be the velocity of swimmer in still water and V_R  be the velocity of flow of river.

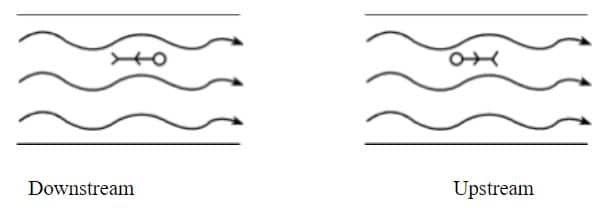
V_total = V_S + V_R V_total = V_S – V_R

In downstream resultant velocity increases while in upstream it decreases.

Relative velocity:

The rate of change of displacement of an object with respect to another object when both are in motion is known as relative velocity of one object w.r.t. another object.

The relative velocity of ‘A’ w.r.t. ‘B’ is 

  $\overrightarrow{{{V}_{AB}}}$=$\overrightarrow{{{V}_{A}}}$ –$\overrightarrow{{{V}_{B}}}$

Let us consider two objects A and B moving with velocities at $\overrightarrow{{{V}_{A}}}$and $\overrightarrow{{{V}_{B}}}$an angle ‘$\theta $’. To find the relative velocity of ‘A’ w.r.t. ‘B’, the velocity of ‘B’ is supposed to be zero. For this, draw a negative vector of  $\overrightarrow{{{V}_{B}}}$ and complete a parallelogram as shown in figure.

The resultant of $\overrightarrow{{{V}_{A}}}$and –$\overrightarrow{{{V}_{B}}}$gives the relative velocity of ‘A’ w.r.t. ‘B’ i.e. $\overrightarrow{{{V}_{AB}}}$

In fig, ‘β’ is the dirⁿ of$\overrightarrow{R}$ (=$\overrightarrow{{{V}_{AB}}}$) with $\overrightarrow{{{V}_{A}}}$

Now, the magnitude of $\overrightarrow{{{V}_{AB}}}$is 

V_AB =$\sqrt{{{V}_{A}}^{2}+2{{V}_{A}}{{V}_{B}}\cos (180-\theta )+{{V}_{B}}^{2}}$

= $\sqrt{{{V}_{A}}^{2}-2{{V}_{A}}{{V}_{B}}\cos \theta +{{V}_{B}}^{2}}$

And,

the direction of $\overrightarrow{{{V}_{AB}}}$ with $\overrightarrow{{{V}_{A}}}$is

α = tan^–1$\left( \frac{{{V}_{B}}\sin (180-\theta )}{{{V}_{A}}+{{V}_{B}}\cos (180-\theta )} \right)$

α = tan^–1$\left( \frac{{{V}_{B}}\sin \theta }{{{V}_{A}}-{{V}_{B}}\cos \theta } \right)$

Special Cases:

(i) When two objects are moving in the same direction i.e. $\theta $=0° then,

V_AB = $\sqrt{{{V}_{A}}^{2}-2{{V}_{A}}{{V}_{B}}\cos {{0}^{o}}+{{V}_{B}}^{2}}$

 = $\sqrt{{{V}_{A}}^{2}-2{{V}_{A}}{{V}_{B}}+{{V}_{B}}^{2}}$

= $\sqrt{{{({{V}_{A}}-{{V}_{B}})}^{2}}}$

$\therefore $V_AB = V_A–V_B

(ii)  When two objects are moving in opposite direction i.e. $\theta $=180° then, 

V_AB = $\sqrt{{{V}_{A}}^{2}-2{{V}_{A}}{{V}_{B}}\cos {{180}^{o}}+{{V}_{B}}^{2}}$

= $\sqrt{{{V}_{A}}^{2}+2{{V}_{A}}{{V}_{B}}+{{V}_{B}}^{2}}$

= $\sqrt{{{({{V}_{A}}+{{V}_{B}})}^{2}}}$

$\therefore $V_AB = V_A+V_B

(iii) When two objects are moving perpendicular to each direction i.e. $\theta $=90°then, 

V_AB = $\sqrt{{{V}_{A}}^{2}-2{{V}_{A}}{{V}_{B}}cos90{}^\circ +{{V}_{B}}2}$

$\therefore $V_AB = $\sqrt{{{V}_{A}}^{2}+{{V}_{B}}^{2}}$

(iv) When two objects are moving with same magnitude velocities:

Let,$\left| \overrightarrow{{{V}_{A}}} \right|$= $\left| \overrightarrow{{{V}_{B}}} \right|$ = V 

then, 

V_AB =$\sqrt{{{V}_{A}}^{2}-2{{V}_{A}}{{V}_{B}}\cos \theta +{{V}_{B}}^{2}}$

= $\sqrt{{{V}^{2}}-2{{V}^{2}}\cos \theta +{{V}^{2}}}$

= $\sqrt{2{{V}^{2}}-2{{V}^{2}}cos\theta }$

= $\sqrt{2{{V}^{2}}(1-\theta cos)}$

= $\sqrt{2{{V}^{2}}.2si{{n}^{2}}\frac{\theta }{2}}$

$\therefore $V_AB = 2Vsin$\frac{\theta }{2}$

Examples of Relative Velocity:

1. The front windscreen of a moving car gets wet in rain while the behind screen remains dry.

2. Rain drops hitting the side of windows of a car in motion often leave diagonal streaks.

3. Person has to incline the umbrella forward with vertical while running in rain. etc.

Q. The front windscreen of a moving car gets wet in rain while the behind screen remains dry. Why?

Answer:

This is due to the relative velocity of rain with respect to the car. 

Let $\overrightarrow{{{V}_{C}}}$ the velocity of the car along the horizontal direction and $\overrightarrow{{{V}_{R}}}$ be the velocity of rain vertically downward. From the above figure, the resultant of $\overrightarrow{{{V}_{R}}}$and –$\overrightarrow{{{V}_{C}}}$gives the relative velocity of rain with respect to the car as shown in the figure above.

Here, Tan$\theta $ = $\frac{p}{b}$= $\frac{AY}{OY}$= $\frac{{{V}_{C}}}{{{V}_{R}}}$

$\therefore $ $\theta $= tan^–1 $\left( \frac{{{V}_{C}}}{{{V}_{R}}} \right)$

So, the raindrop strikes the front windscreen making an angle $\theta $= tan^{–1$\left( \frac{{{V}_{C}}}{{{V}_{R}}} \right)$}with vertical direction. Thus, the front windscreen of a moving car gets wet in rain while behind the screen remains dry.

Numerical Problems (Kinematics)

Take acceleration due to gravity, g = 10 ms^–2

Q.1 A car travelling with a speed of 15m/s is braked and it slows down with uniform retardation. It covers a distance of 88 m as its velocity reduces to 7m/s. If the car continues to slow down with the same rate, after what further distance will it be brought to rest?  Ans: 24.5 m

Q.2 A body falls freely from the top of a tower and during the last second of its fall, it falls through 25m. Find the height of tower.   Ans: 45 m

Q.3 An object is dropped from the top of the tower of height 156.8 m. and at the same time another object is   thrown vertically upward with the velocity of 78.1 m/s from   the foot of the tower, when and where the object meet?            Ans: 2 sec. and 20 m below from top

Q.4 An object is dropped from the top of the tower of height 100m and after 2 sec another object is thrown vertically upward with velocity 25 m/s from the foot of the tower. When and where the objects meet?

Ans: after 3 sec of 1^st object dropped, 45m below the top.

Q.5 A swimmer’s speed along the river (down-stream) is 20 km/h and can swim up-stream at 8 km/h. Calculate the velocity of the stream and the swimmer’s possible speed in still water.          Ans: 14 km/hr, 6 km/hr

Q.6 A swimmer’s speed along the river is 20 kmph and up-stream is 8 kmph. Calculate the velocity of the stream and the swimmer’s possible speed in still water.     Ans: 14 km/hr, 6 krnihr

Q.7 A man wishes to swim across a river 600m wide. If he can swim at the rate of 4km/h in still water and the river flows at 2km/h. Then in what direction must he swim to reach a point exactly opposite to the starting point and when will he reach it?         Ans: 120° with water and 10.4 min

Q.8 A projectile is fired from ground level with a velocity 500 ms^-1 at 30^o to the horizontal. Find the horizontal range, the greatest height and the time to reach the greatest height.     Ans:  21651m, 3125m, 25 sec

Q.9 A baseball is thrown towards a player with an initial velocity 20 ms^-1at 45^o with the horizontal. At the moment, the ball is thrown the player is 50 m from the thrower. At what is speed and in what direction must he run to catch the ball at the same height at which it is released?          Ans: 3.5 ms^-1 towards the thrower

Q.10 A body is projected upwards making an angle $\theta $ with the horizontal with a velocity of 300 m/s. Find the value of $\theta $ so that the horizontal range will be maximum. Find its range and time of flight.  Ans: 45°, 9000 m

Q.11 A stone on the top of a vertical cliff is kicked horizontally so that its initial velocity is 9 ms^-1. If the cliff is 200 m high, calculate

(i) taken by the stone to reach the ground.

(ii) How far from the bottom of the cliff, the stone will hit the ground?       Ans: (i) 6.32 sec (ii) 56.92 m

Q.12 A stone on the edge of a vertical cliff is kicked so that its initial velocity is 9 m/s horizontally. If the cliff is 200m high, calculate: i. time taken by stone to reach the ground. ii. How far from the cliff the stone will hit the ground?                  Ans: (i) 6.32 sec (ii) 56.92 m

Q.13 A bullet is fired with a velocity of 100 m/s from the ground at an angle of 60° with the horizontal. Calculate the horizontal range covered by the bullet. Also calculate the maximum height attained.                Ans: 866m; 375 m

Q.14 A projectile is fired from the ground level with velocity 150 m/s at 30° to the horizontal. Find its   horizontal range. What will be the least speed with which it can.be projected to achieve the same horizontal range?       Ans: 1949 m, 140 m/s

Q.15 A projectile is fired from the ground level with velocity of 500 m/s at 30° to horizon. Find the horizontal range, and greatest vertical height to which it rises. What is   the least speed with which it could be projected in order to   achieve the same horizontal range? [g = 10 N kg^-1]     Ans: 21651 m, 3125 m, 464 ms^-1

Q.16 A body is projected horizontally from the top of   a tower 100 m high with a velocity of 9.8 ms^-1. Find the velocity with which it hits the ground.      Ans: 45.82 m/s at 77.9°

Q.17 A batter hits a baseball so that it leaves the bat with an initial speed 37m/s at an angle of 53°. Find the position of the ball and the magnitude and direction of its velocity after 2 seconds. Treat the baseball as a projectile.         Ans: 24.23 m/sec, 23.21°

Q.18 A stone is projected horizontally with 20m/s from top of a tall building. Calculate its position and velocity after 3 sec neglecting the air resistance.        Ans: 36 m/sec; 56.3°

Q.19 A projectile is launched with an initial velocity of 30 m/s at an angle of 60° above the horizontal. Calculate the magnitude and direction of its velocity 5s after launch. Ans: 28.3 m/s and 58° C from horizontal

Q.20 An airplane is flying with a velocity of 90 m/s at an angle of 23.0° above the horizontal. When the plane is 114 m directly above a dog that is standing on level ground, a suitcase drops out of luggage compartment far from the dog will the suitcase land? You can ignore it resistance.            Ans: 778.7 m from dog

Q.21 To a cyclist riding due west with a speed of 4 m/s, a wind appears to blow from south west. The wind appears to blow from south to a man, running at 2ms^-1 in the same direction. What is the actual velocity of the wind?  Ans: 2$\sqrt2$ ms^-1 from south east

Q.22 To a person going due east in a car with a velocity 25 km/hr, a train appear to move due north with a velocity of 25$\sqrt3$ km/hr. What is the actual velocity and direction of motion of train?

Ans: 50 km/hr along a direction 30° east of north.

Q.23 Two ships A and B are moving in a sea. If A moves with uniform velocity of 8 kmhr^–1 due east B moves with uniform velocity 6 kmhr^–1 due south. Calculate the relative velocity of ship A with respect to ship B.

Also Read: Vector Notes Class 11