Vectors Class 11 Physics | Notes

All physical quantities can be broadly classified into two categories: vector quantity and scalar quantity.

Vector Quantity:

A physical quantity which has both magnitude and direction and obeys the rules of vector algebra is known as vector or vector quantity. It is denoted by alphabetical letter(s) with an arrow- head over it.

Electric current and pressure have both magnitude and direction but they do not obey the rules of vector algebra. So, electric current and pressure are scalar quantities (not vector). 

For Example: displacement, velocity, acceleration, force etc.

Scalar Quantity:

A physical quantity which has magnitude only but no direction is called a scalar quantity. Scalar quantity obeys the rules of simple algebra (scalar algebra). It is denoted by an alphabetical letter.

For Example: mass, length, time, distance, speed etc.

Representation of a vector:

Any vector ($\overrightarrow{a}$) can be expressed as

$\overrightarrow{a}$ = a₁$\widehat{i}$ + a₂$\widehat{j}$ + a₃$\widehat{k}$

Where a₁, a₂ and a₃ are components of $\overrightarrow{a}$ along X, Y and Z-axis respectively and $\widehat{i}$, $\widehat{j}$ and $\widehat{k}$ are unit vectors along X, Y and Z-axis respectively.

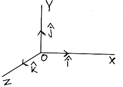
Modulus/Magnitude of a vector:

The modulus of any vector $\overrightarrow{a}$ = x$\widehat{i}$ + y$\widehat{j}$ + z$\widehat{k}$ is denoted by $\left| \overrightarrow{a} \right|$ and given by:

$\left| \overrightarrow{a} \right|$ = $\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}$ unit.

Q. Find the magnitude (modulus) of given vector $\overrightarrow{a}$ = 3$\widehat{i}$ – 2$\widehat{j}$ + $\widehat{k}$.

Solution: The given vector is $\overrightarrow{a}$ = 3$\widehat{i}$ – 2$\widehat{j}$ + $\widehat{k}$.

Then modulus of $\overrightarrow{a}$ is

$\left| \overrightarrow{a} \right|$ = $\sqrt{{{3}^{2}}+{{(-2)}^{2}}+{{1}^{2}}}$

= $\sqrt{9+4+1}$

= $\sqrt{14}$ unit.

Types of vector:

1. Unit vector:

A vector which has magnitude one (unity) is called unit vector. It is denoted by an alphabetical letter with the cap over it.

 Example:   $\widehat{a}$, $\widehat{b}$, $\widehat{i}$, $\widehat{j}$ ,$\widehat{k}$ etc. Mathematically, the unit vector along a vector, $\overrightarrow{a}$ is given by

$\widehat{a}$ = $\frac{\overrightarrow{a}}{\left| \overrightarrow{a} \right|}$

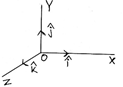
 $\widehat{i}$, $\widehat{j}$ and $\widehat{k}$ are the unit vectors along x, y and z – axis respectively.                                               

Q. Find the unit vector along (of) $\overrightarrow{a}$ = 2$\widehat{i}$ – $\widehat{j}$ + 2$\widehat{k}$.

Solution: The given vector is $\overrightarrow{a}$ = 2$\widehat{i}$ – $\widehat{j}$ + 2$\widehat{k}$.

The modulus of$\overrightarrow{a}$ is

$\left| \overrightarrow{a} \right|$ = $\sqrt{{{\mathbf{2}}^{2}}+{{(-\mathbf{1})}^{2}}+{{\mathbf{2}}^{2}}}$

= $\sqrt{\mathbf{4}+\mathbf{1}+\mathbf{4}}$ = $\sqrt{\mathbf{9}}$ = 3 unit.

Now, the unit vector along $\overrightarrow{a}$ is given by

$\widehat{a}$ = $\frac{\overrightarrow{a}}{\left| \overrightarrow{a} \right|}$

$\text{ }$= $\frac{2\widehat{i}-\widehat{j}+2\widehat{k}}{3}$

$\text{ }$= $\frac{2}{3}$$\widehat{i}$ –$\frac{1}{3}$ $\widehat{j}$ + $\frac{2}{3}$$\widehat{k}$.

A Quick Question For You: Find the magnitude of $\overrightarrow{b}$= $\frac{2}{3}$$\widehat{i}$ –$\frac{1}{3}$ $\widehat{j}$ + $\frac{2}{3}$$\widehat{k}$. [Ans: 1]

2. Null vector:

A vector which has magnitude zero is called null vector. This vector is generally used to indicate the direction of physical quantity. i.e $\overrightarrow{a}$ is null vector if $\left| \overrightarrow{a} \right|$ = 0

3. Parallel vector:

Two vectors of the same or different magnitude are said to be parallel vectors if they act in the same direction.

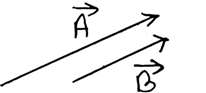
In figure, $\overrightarrow{A}$ and $\overrightarrow{B}$ are parallel vectors.

4. Anti-parallel vectors (Unlike Parallel):

Two vectors of same and opposite magnitude are said to be anti-parallel vectors if they act in the opposite direction.

In figure, $\overrightarrow{A}$ and $\overrightarrow{B}$ are anti-parallel vectors.

5. Equal vectors:

Two vectors are said to be equal vectors if they have equal magnitude and act in the same direction.

In figure, $\overrightarrow{A}$ and $\overrightarrow{B}$  are equal vectors.

6. Negative vector:

The negative vectors of $\overrightarrow{A}$ is defined as a vector which has equal magnitude and opposite direction to that of $\overrightarrow{A}$.

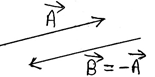
In figure, $\overrightarrow{A}$ and $\overrightarrow{B}$ are negative vectors of each other. 

7. Collinear vectors:

Two or more vectors are said to be collinear if they act along the same straight line. 

In figure, $\overrightarrow{A}$ , $\overrightarrow{B}$ and $\overrightarrow{C}$ are collinear vectors.

8. Coplanar vectors:

Two or more vectors are said to be coplanar if they act on a same plane.

In figure, $\overrightarrow{A}$, $\overrightarrow{B}$ and $\overrightarrow{C}$ are coplanar vectors.

9. Position Vectors:

A vector whose initial point is origin and terminal point be any point ‘P’

In figure, $\overrightarrow{OA}$ = $\overrightarrow{r}$ be the position vector of point ‘P’.

10. Co-initial vectors:

Two or more vectors are said to be co- initial if they have the same starting point.

In figure, $\overrightarrow{A}$ and $\overrightarrow{B}$ are co-initial vectors.

11. Co- terminal vectors:

Two or more vectors are said to be co- terminal if they have the same terminal (final) point.

In figure, $\overrightarrow{A}$ , $\overrightarrow{B}$ and $\overrightarrow{C}$ co- terminal vectors. 

12. Orthogonal vectors:

Two vectors are said to be orthogonal if they are perpendicular to each other.

In figure, $\overrightarrow{A}$ and $\overrightarrow{B}$ are orthogonal vectors. 

Composition of vectors:

The process of obtaining a single vector from two or more vectors is called the composition of vectors. 

The single vector obtained as a result is called the resultant vector.

Triangle Law of vector addition:

Statement: When two vectors acting simultaneously at a point be represented by two sides of a triangle taken in same order both in magnitude and direction then the third side taken in reverse order represents their resultant both in magnitude and direction.

Proof:

Let us consider two vectors acting simultaneously at a point be represented by two sides AB and BC of triangle ABC taken in same order both in magnitude and direction.

According to triangle law of vector addition, third side AC taken in reverse order represents their resultant both in magnitude and direction i.e. $\overrightarrow{AC}$ = $\overrightarrow{R}$ = $\overrightarrow{P}$ + $\overrightarrow{Q}$. Let us produce AB to N and draw CN perpendicular to it (AN). Let the angle between two vectors $\overrightarrow{P}$ and $\overrightarrow{Q}$ be

$\angle $CBN=$\theta $ and

$\alpha $ = $\angle $CAB be the direction of resultant vector with first vector $\overrightarrow{P}$.

In right angled $\Delta $ BNC,

sin$\theta $ = $\frac{CN}{BC}$ =$\frac{CN}{Q}$ $\therefore $CN = Qsin$\theta $

& cos$\theta $ = $\frac{BN}{BC}$ = $\frac{BN}{Q}$ $\therefore $BN = Qcos$\theta $

Now, in right angled $\Delta $ ANC,

h²= p² + b²

Or, (AC)² = (CN)² + (AN)²

Or, R² = (Qsin$\theta $)² + (AB+ BN)²

Or, R² = Q²sin$\theta $² + (P+ Qcos$\theta $)²

Or, R² = Q²sin$\theta $² + P²+2PQcos$\theta $ + Q²cos$\theta $²

Or, R² = P²+2PQcos$\theta $ +Q²(sin²$\theta $ + cos²$\theta $)

Or, R² = P²+2PQcos$\theta $ +Q²

Or, R = $\sqrt{{{P}^{2}}+2PQcos\theta +{{Q}^{2}}}$

which is the required expression for magnitude of resultant vector.

Again in right angled $\Delta $ANC

tan$\alpha $ = $\frac{CN}{AN}$

or, tan$\alpha $ = $\frac{Qsin\theta }{P+Qcos\theta }$

or, $\alpha $ = tan^-1($\frac{Qsin\theta }{P+Qcos\theta }$), which is the required direction of resultant vector $\overrightarrow{R}$ with first vector $\overrightarrow{P}$.

Parallelogram law of vector addition:

Statement: When two vectors acting simultaneously at a point be represented by two adjacent sides of a parallelogram starting from the same point both in magnitude and direction then the diagonal starting from the same point represents their resultant both in magnitude and direction.

Proof:

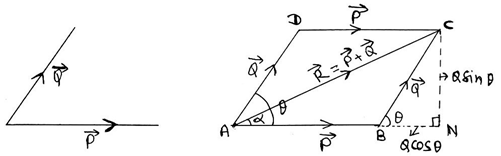
Let us consider two vectors $\overrightarrow{P}$ and $\overrightarrow{Q}$ acting simultaneously at a point be represented by two adjacent sides AB and AD starting from the same point of a parallelogram ABCD both in magnitude and direction. According to the parallelogram law of vector addition, the diagonal AC starting from the same point represents their resultant both in magnitude and direction.

i.e. $\overrightarrow{AC}$ = $\overrightarrow{R}$ = $\overrightarrow{P}$ + $\overrightarrow{Q}$. Let us produce AB to N and draw CN perpendicular to it (AN). Let the angle between two vectors $\overrightarrow{P}$ and $\overrightarrow{Q}$ be $\angle $BAD = $\theta $ and

$\alpha $ = $\angle $CAB be the direction of resultant vector with first vector $\overrightarrow{P}$.

$\overrightarrow{BC}$ = $\overrightarrow{AD}$ = $\overrightarrow{Q}$ [being the opposite sides of parallelogram ABCD]

$\angle $CBN = $\angle $BAD = $\theta $ [being corresponding angles between parallel lines BC and AD]

In right angled $\Delta $ BNC,

sin$\theta $ = $\frac{CN}{BC}$ =$\frac{CN}{Q}$ $\therefore $CN = Qsin$\theta $

& cos$\theta $ = $\frac{BN}{BC}$ = $\frac{BN}{Q}$ $\therefore $BN = Qcos$\theta $

Now, in right angled $\Delta $ ANC,

h² = p² + b²

Or, (AC)² = (CN)² + (AN)²

Or, R² = (Qsin$\theta $)² + (AB+ BN)²

Or, R² = Q²sin$\theta $² + (P+ Qcos$\theta $)²

Or, R² = Q²sin$\theta $² + P²+2PQcos$\theta $ + Q²cos$\theta $²

Or, R² = P²+2PQcos$\theta $ +Q²(sin²$\theta $ + cos²$\theta $)

Or, R² = P²+2PQcos$\theta $ +Q²

Or, R = $\sqrt{{{P}^{2}}+2PQcos\theta +{{Q}^{2}}}$

which is the required expression for magnitude of resultant vector.

Again in right angled $\Delta $ANC

tan$\alpha $ = $\frac{CN}{AN}$

or, tan$\alpha $ = $\frac{Qsin\theta }{P+Qcos\theta }$

or, $\alpha $ = tan^-1($\frac{Qsin\theta }{P+Qcos\theta }$), which is the required direction of resultant vector $\overrightarrow{R}$ with first vector $\overrightarrow{P}$.

Special cases:

(i) When two vectors act in the same direction i.e. $\theta $=0°

This is the condition of maximum value of magnitude of $\overrightarrow{R}$.

i.e. R = P + Q

The direction of the resultant vector is same as that of $\overrightarrow{P}$ and $\overrightarrow{Q}$.

(ii) when two vectors act in the opposite direction i.e.d$\theta $ =180°

then R = $\sqrt{{{P}^{2}}+2PQcos\theta +{{Q}^{2}}}$

R = $\sqrt{{{P}^{2}}+2PQcos{{180}^{\circ }}+{{Q}^{2}}}$

R = $\left| P-Q \right|$

This is the condition of minimum value of magnitude of $\overrightarrow{R}$. The direction of the resultant is same as that of larger vector.

(iii) When two vectors act perpendicular to each other i.e. $\theta $ = 90°

then R = $\sqrt{{{P}^{2}}+2PQcos\theta +{{Q}^{2}}}$

R = $\sqrt{{{P}^{2}}+2PQcos{{90}^{\circ }}+{{Q}^{2}}}$

R = $\sqrt{{{P}^{2}}+{{Q}^{2}}}$ is the magnitude of $\overrightarrow{R}$

The direction of resultant $\overrightarrow{R}$ is in between $\overrightarrow{P}$ and $\overrightarrow{Q}$, slanted towards the larger vector.

(iv) When two vectors have equal magnitude. $\left| \overrightarrow{P} \right|$ = $\left| \overrightarrow{Q} \right|$ = x

then R = $\sqrt{{{P}^{2}}+2PQcos\theta +{{Q}^{2}}}$

R = $\sqrt{{{x}^{2}}+2xxcos\theta +{{x}^{2}}}$

R = $\sqrt{2{{x}^{2}}+2{{x}^{2}}cos\theta }$

R = $\sqrt{2{{x}^{2}}(1+\cos \theta )}$

R = 2x cos$\frac{\theta }{2}$ is the magnitude of $\overrightarrow{R}$. The direction of $\overrightarrow{R}$ is exactly in between $\overrightarrow{P}$ and $\overrightarrow{Q}$. i.e. $\alpha $ = $\frac{\theta }{2}$

Polygon law of vector addition:

It states that when a number of vector acting simultaneously at a point be represented by different sides of a polygon taken in same order both in magnitude and direction then, the closing side of polygon taken in reverse order represents the resultant both in magnitude and direction.

Let us consider five vectors $\overrightarrow{A}$, $\overrightarrow{B}$, $\overrightarrow{C}$, $\overrightarrow{D}$ and $\overrightarrow{E}$ acting simultaneously at a point be represented by different (n-1) sides of a polygon OA, AB, BC, CD, DE taken in same order both in magnitude and direction then the closing side (n^th) of the polygon taken in reverse order represents their resultant both in magnitude and direction. 

i.e. $\overrightarrow{OA}$ + $\overrightarrow{AB}$ + $\overrightarrow{BC}$ + $\overrightarrow{CD}$ + $\overrightarrow{DE}$ = $\overrightarrow{OE}$

$\overrightarrow{A}$ + $\overrightarrow{B}$ + $\overrightarrow{C}$ + $\overrightarrow{D}$ + $\overrightarrow{E}$ = $\overrightarrow{R}$

Subtraction of vectors: When $\overrightarrow{B}$ is subtracted from $\overrightarrow{A}$ then using parallelogram law of vector addition the resultant vector $\overrightarrow{R}$ i.e. ($\overrightarrow{A}$ – $\overrightarrow{B}$) can be obtained as

Resolution of a vector:

The process of splitting a vector into its constituent components is called resolution of a vector.

If resolution of a vector is carried out in such a way that the two components are perpendicular to each other then the components are known as rectangular components of the vector.

Let the vector $\overrightarrow{A}$ be represented by the side OA both in magnitude and direction.

Let the vector $\overrightarrow{A}$ has A_x and A_y components along horizontal and vertical direction such that OB = A_x and OC= A_y

Let ‘$\theta $’ be the direction of $\overrightarrow{A}$ with positive x-axis.

Let us complete a parallelogram OBAC as shown in figure.

From figure,

BA = OC = A_y

Now,

X-component of $\overrightarrow{A}$, A_x= Acos$\theta $……..(i)

Y-component of $\overrightarrow{A}$, A_y= Asin$\theta $……..(ii)

Squaring and adding eqn (i) and (ii)

A_x²+ A_y²= A²[(cos$\theta $)² +(sin$\theta $)²]

A_x²+ A_y²= A²

A = $\sqrt{\mathbf{A}_{x}^{2}+\mathbf{A}_{y}^{2}}$ is magnitude of $\overrightarrow{A}$ in terms of its rectangular components.

Similarly, tan$\theta $ = $\frac{AB}{OB}$ = $\frac{{{A}_{y}}}{{{A}_{x}}}$

$\theta $ = tan^-1($\frac{{{A}_{y}}}{{{A}_{x}}}$) is the direction of $\overrightarrow{A}$ in terms of its rectangular components.

Multiplication of a vector

(i) Multiplication of a vector by a number:

When $\overrightarrow{a}$ is multiplied by a number (n) the result n$\overrightarrow{a}$ is a vector quantity whose magnitude is ‘n’ times that of $\overrightarrow{a}$ and direction is same as that of $\overrightarrow{a}$.

(ii) Multiplication of a vector by a scalar:

When $\overrightarrow{a}$ is multiplied by a scalar ‘m’ (say) the result, m$\overrightarrow{a}$ is a vector quantity. In this case the product obtained is a new physical quantity which has the same direction as that of $\overrightarrow{a}$.

For example, m$\overrightarrow{a}$=$\overrightarrow{F}$ where m is mass, $\overrightarrow{a}$ is the acceleration and $\overrightarrow{F}$is force.

(iii) Multiplication of a vector by another vector:

a. Dot product (Scalar product):

The dot product of two vectors $\overrightarrow{a}$ and $\overrightarrow{b}$ is denoted by$\overrightarrow{a}$.$\overrightarrow{b}$ and given by$\overrightarrow{a}$.$\overrightarrow{b}$ = a b cos$\theta $

where ‘$\theta $’ be the angle between two vectors $\overrightarrow{a}$ and $\overrightarrow{a}$.

The dot product of two vectors in a scalar quantity that is why it is also called a scalar product.

Also, if $\overrightarrow{a}$ = a₁$\widehat{i}$ + a₂$\widehat{j}$ + a₃$\widehat{k}$ and $\overrightarrow{b}$ = b₁$\widehat{i}$ + b₂$\widehat{j}$ + b₃$\widehat{k}$

then$\overrightarrow{a}$.$\overrightarrow{b}$ = a₁b₁ + a₂b₂+ a₃b₃

Properties of scalar / dot product.

1. The dot product of $\overrightarrow{a}$ and $\overrightarrow{b}$ is maximum when $\theta $ = 0°

i.e. $\overrightarrow{a}$.$\overrightarrow{b}$ = a b cos0°= ab (Maximum)

2. A dot product of a and b is zero when if $\theta $ = 90°

i.e. $\overrightarrow{a}$.$\overrightarrow{b}$ = a b cos90°= 0

3. The scalar / dot product of two vectors $\overrightarrow{a}$ and $\overrightarrow{b}$ follows commutative law$\overrightarrow{a}$.$\overrightarrow{b}$ = $\overrightarrow{b}$.$\overrightarrow{a}$

4. The dot product of two vectors $\overrightarrow{a}$ and $\overrightarrow{b}$ follows distributive law. i.e. $\overrightarrow{a}$.($\overrightarrow{b}$+$\overrightarrow{c}$) =$\overrightarrow{a}$.$\overrightarrow{b}$ +$\overrightarrow{a}$.$\overrightarrow{c}$

5. The square of a vector is a scalar quantity.

i.e. ($\overrightarrow{a}$)² =$\overrightarrow{a}$.$\overrightarrow{a}$ = a a cos0°= a²

$\therefore $ ($\overrightarrow{a}$)² = a² is a scalar quantity.

Scalar / dot product of unit vectors.

(i) $\widehat{i}$ . $\widehat{i}$ = $\left| \widehat{i} \right|\text{ }\left| \widehat{i} \right|$cos0°= 1 i.e. $\widehat{i}$ . $\widehat{i}$ = $\widehat{j}$.$\widehat{j}$= $\widehat{j}$ + $\widehat{k}$. $\widehat{k}$ = 1

(ii) $\widehat{i}$. $\widehat{j}$= $\left| \widehat{i} \right|\text{ }\left| \widehat{j} \right|$cos90°= 0 i.e. $\widehat{i}$ . $\widehat{j}$= $\widehat{j}$.$\widehat{k}$+ $\widehat{k}$. $\widehat{i}$ = 0

b. Cross product (Vector product) of two vectors:

The vector (cross) product of two vectors $\overrightarrow{a}$ and $\overrightarrow{b}$ is denoted by $\overrightarrow{a}$×$\overrightarrow{b}$ and given by

$\overrightarrow{a}$×$\overrightarrow{b}$ = $\left| \overrightarrow{a} \right|$ $\left| \overrightarrow{b} \right|$ sin$\theta $ $\widehat{n}$

= a b sin$\theta $ $\widehat{n}$

where, a b sin$\theta $ is the magnitude of $\overrightarrow{a}$×$\overrightarrow{b}$ and and ‘$\widehat{n}$’ is its direction which is perpendicular to both $\overrightarrow{a}$ and $\overrightarrow{b}$.

The direction of $\overrightarrow{a}$×$\overrightarrow{b}$ is obtained by right hand thumb rule or right hand screw rule.

The vector $\overrightarrow{a}$×$\overrightarrow{b}$ is perpendicular to both $\overrightarrow{a}$ and $\overrightarrow{b}$. Since, the cross product of $\overrightarrow{a}$ and $\overrightarrow{b}$ is again a vector so, it is also called vector product.

if $\overrightarrow{a}$ = a₁$\widehat{i}$ + a₂$\widehat{j}$ + a₃$\widehat{k}$ and $\overrightarrow{a}$ = b₁$\widehat{i}$ + b₂$\widehat{j}$ + b₃$\widehat{k}$

$\overrightarrow{a}$ = (a₂b₃– a₃b₂) $\widehat{i}$ +(a₃b₁– a₁b₃) $\widehat{j}$ + (a₁b₂– a₂b₁)$\widehat{k}$

Properties of vector / cross product:

1. The magnitude of vector product is maximum if $\theta $ = 90°

    i.e. $\left| \overrightarrow{a}\times \overrightarrow{b} \right|$ = a b sin90°= ab (max^m)

1. Similarly,  the magnitude of vector product is zero if $\theta $ = 0°
2. i.e. $\left| \overrightarrow{a}\times \overrightarrow{b} \right|$ = a b sin0°= 0 (zero)
3. The vector product does not obey commutative law.

     i.e. $\overrightarrow{a}\times \overrightarrow{b}\ne \overrightarrow{b}\times \overrightarrow{a}$ but $\vec{a}\times \vec{b}=-(\vec{b}\times \vec{a})$

     4. The vector product always obeys distributive law.

     i.e. $\overrightarrow{a}\times (\overrightarrow{b}+\overrightarrow{c}\text{)=}\overrightarrow{a}\times \overrightarrow{b}+\overrightarrow{a}\times \overrightarrow{c}$

     5. The magnitude of cross product of a vector with itself is zero i.e.

$\left| \overrightarrow{a}\times \overrightarrow{a} \right|$= a a sin0° = 0 (zero)

Physical Significance (geometrical meaning) of vector product: 

If two vector $\overrightarrow{a}$ and $\overrightarrow{b}$ are represented by two adjacent sides of a parallelogram both in magnitude and direction then the magnitude of $\overrightarrow{a}$×$\overrightarrow{b}$ gives the area of that parallelogram.

i.e. $\left| \overrightarrow{a}\times \overrightarrow{b} \right|$ = ab sin$\theta $ = area of parallelogram OACB.

Some important numerical problems of Vector:

Q.1 A disoriented physics professor drives 3.25 km north, then 4.75 km west and then 1.50 km south. Find the magnitude and direction of the resultant displacement.

Ans: 5.06km, 20.22^o north of west (or 69.78^o W of N).

Q.2 A spelunker is surveying a cave. She follows a passage of 180m straight west, then 210m in a direction 45^o east of south, and then 280m at 30^o east of north. After a fourth unmeasured displacement she finds herself back where she started. Use the method of components to determine the magnitude and direction of the fourth displacement.

Ans: 144m, 41^o S of W.

Q. 3 A cave explorer is surveying a cave. He follows a passage 100m straight east, then 50m in a direction 30^o west of north, then 150m at 45^o west of south. After a fourth unmeasured displacement he finds himself back where he started. Using a scale drawing to determine the forth displacement (magnitude and direction).

Ans: 70.02m in the direction 26.34^o east of north.

Q. 4 A rocket fires two engines simultaneously. One produces a thrust of 725N directly forward, while the other gives a 513N thrust at 32.4^o above the forward direction. Find the magnitude and direction of the resultant force that these engines exert on the rocket.

Ans: 1119N and direction 13.4^o.

Also Read: Kinematics: Notes Class 11 | Physics (Part-I)