Dynamics | Laws Of Motion Class 11 | Physics | Notes

Force

Force is defined as an external agent that can change or tries to change the state of rest or uniform motion of an object. It’s unit is Newton (N) in S.I. and Dyne in C.G.S. It is a vector quantity.

1N = 10⁵ dyne

Inertia 

The tendency of an object to remain in its own state of rest or uniform motion is called inertia. 

Types of inertia 

(i) Inertia of rest

(ii) Inertia of motion 

(iii) Directional inertia 

Newton’s first law of motion 

Everybody in the universe continues in its own state of rest or uniform motion unless an external force acts upon it. 

i.e. for F_external = 0, u = v 

Q. Newton’s first law of motion gives the definition of force and inertia. Justify. 

Solution: 

Newton’s first law of motion describes force in a qualitative way. According to the first law of motion, an object cannot change its state of rest or uniform motion without an external force. Thus, it can be concluded that force is an external agent that causes a body to change its state (rest or uniform motion). Thus, Newton’s first law of motion defines force and inertia. 

Momentum (Linear momentum,$\overrightarrow{P}$) 

It is defined as the total motion contained in a body. It is denoted by$\overrightarrow{P}$ and mathematically given by

$\overrightarrow{P}$ = mass × velocity 

= m × v

It’s unit is kgms^–1.

Newton’s second law of motion 

It states that the rate of change of momentum of a body is directly proportional to the force applied on it,

i.e.  $\frac{\Delta p}{\Delta t}$$\propto $ F 

Let us consider an object of mass ‘m’ moving with velocity ‘u’ at position A, and ‘a’ be its uniform acceleration. After time ‘t’, let the velocity of the object become ‘v’ at position B. 

Now, initial momentum = m.u

final momentum = m.v

change in momentum = mv – mu

Rate of change in momentum = $\frac{mv-mu}{t}$

According to Newton’s second law of motion, rate of change of momentum is directly proportional to the force applied on it,

i.e. $\frac{mv-mu}{t}$ $\propto $ F 

or, $\frac{m(v-u)}{t}$ $\propto $ F 

or, ma $\propto $ F 

or, ma = kF,   [where K is proportionality constant, for K = 1]

$\therefore F=ma$

Thus, Newton’s second law of motion gives the quantitative definition of force.

By knowing the values of ‘m’ and ‘a’, force can be calculated. 

Q. Newton’s second law of motion gives the measurement of force. Justify.

Impulse (I)

It is defined as the force acting upon an object for a very short time that changes the momentum. The short time for which the objects remain in contact is known as time of impact. Impulse is denoted by ‘I’ and mathematically given by 

I = F × $\Delta $t

= ma × $\Delta $t

= $\frac{m(v-u)}{\Delta t}$ × $\Delta $t 

Or, I = mv – mu

$\therefore $I = P_f  – P_i

Thus, numerically impulse is equal to change in momentum.

Newton’s third law of motion 

It states that to every action, there is an equal and opposite reaction.

Let us consider two objects A and B collide with each other. Let F_BA and F_AB be the forces exerted by A on B and by B on A respectively. Then, according to Newton’s third law of motion. 

F_BA = – F_AB 

(i) Derivation of first law of motion from second law 

From Newton’s second law of motion,

F = $\frac{dp}{dt}$ = $\frac{m(v-u)}{t}$

In the absence of external force, i.e. F = 0, 

We have, 

Or, 0 = $\frac{m(v-u)}{t}$ 

or, v – u = 0 

$\therefore $ v = u

i.e. an object continues in its own state (rest or uniform motion, u = v) in the absence of external force. This is Newton’s first law of motion.

(ii) Derivation of third law of motion from second law 

From Newton’s second law of motion, 

F = $\frac{dp}{dt}$ = $\frac{\Delta p}{\Delta t}$ ………. (i)

Let us consider two bodies A and B of masses ‘m₁‘ and ‘m₂‘ are moving with initial velocities ‘u₁‘ and ‘u₂‘ respectively such that u₁ is greater than u₂. They collide after some time and move separately with final velocities ‘v₁‘ and ‘v₂‘ respectively. During the collision, let F_BA be the force exerted by A on B and F_AB be the force exerted by B on A respectively.

From Newton’s second law of motion,

F_AB = $\frac{d{{P}_{A}}}{dt}$ = $\frac{\Delta {{P}_{A}}}{t}$

$\therefore $ $\Delta $P_A = F_AB × t ……….. (ii) 

And, F_BA = $\frac{d{{P}_{B}}}{dt}$ = $\frac{\Delta {{P}_{B}}}{t}$ 

$\therefore $ $\Delta $P_B = F_BA × t ………… (iii)

$\therefore $ Total change in momentum of A and B, $\Delta $P = $\Delta $P_A + $\Delta $P_B   

In the absence of external force i.e. F_ext = 0 

then from equation (i) we have,

$\Delta P$ = 0 

$\therefore $ $\Delta $P_A + $\Delta $P_B = 0 

From (i), (ii) and (iii)

F_AB × t + F_BA × t = 0 

Or, t (F_AB + F_BA) = 0 

$\therefore $F_AB = – F_BA

i.e. two forces F_AB and F_BA are equal in magnitude and opposite in direction. This is Newton’s third law of motion. Since Newton’s first and third laws can be derived from the second law of motion. So Newton’s second law is the real law

Q. Newton’s second law is the real law. Explain.Or

Q. Derive of Newton’s first and third law from the second law of motion. 

Principle of Conservation of Linear Momentum:

Statement:

It states that in the absence of external force, the total linear momentum of an isolated system remains constant.

OR

In collision, the sum of linear momentum before collision is equal to the sum of linear momentum after collision in the absence of external force. 

Proof: 

 Let us consider two bodies A and B of masses ‘m₁‘ and ‘m₂‘ are moving with initial velocities ‘u₁‘ and ‘u₂‘ respectively such that u₁ is greater than u₂. They collide after some time and move separately with final velocities ‘v₁‘ and ‘v₂‘ respectively. During the collision, let F_BA be the force exerted by A on B and F_AB be the force exerted by B on A respectively.

Now, 

initial momentum of A = m₁u₁  

initial momentum of B = m₂u₂ 

final momentum of A = m₁v₁ 

final momentum of B = m₂v₂ 

change in momentum of A = m₁v₁ – m₁u₁ 

change in momentum of B = m₂v₂ – m₂u₂

Then,

Rate of change of momentum of A = $\frac{{{m}_{1}}{{v}_{1}}-{{m}_{1}}{{u}_{1}}}{t}$

Rate of change of momentum of B = $\frac{{{m}_{2}}{{v}_{2}}-m{}_{2}{{u}_{2}}}{t}$

According to Newton’s second law of motion.

Force exerted by A on B = rate of change of momentum of B.

i.e. F_BA =  $\frac{{{m}_{2}}{{v}_{2}}-m{}_{2}{{u}_{2}}}{t}$……… (i) 

Force exerted by B on A = rate of change of momentum of A 

i.e. F_AB =   $\frac{{{m}_{1}}{{v}_{1}}-{{m}_{1}}{{u}_{1}}}{t}$……… (ii)

According to Newton’s third law of motion,

  F_BA = – F_AB 

 Or, $\frac{{{m}_{2}}{{v}_{2}}-m{}_{2}{{u}_{2}}}{t}$ = $\frac{-(m{}_{1}{{v}_{1}}-{{m}_{1}}{{u}_{1}})}{t}$

or, – m₁v₁ + m₂u₂ = m₂v₂ – m₁u₁

$\therefore $ m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂,

i.e. the sum of linear momentum before collision is equal to the sum of momentum after collision which is the principle of conservation of linear momentum.

Some applications of conservation of linear momentum 

1. Motion of gun and bullet 

Let us consider a gun and a bullet of masses m₁ and m₂ respectively are at rest before firing. After firing, let the gun and the bullet move with velocities v₁ and v₂. From conservation of linear momentum,

m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂ 

Since, u₁ = u₂ = 0 

m₁v₁ + m₂v₂ = 0 

$\therefore {{v}_{1}}=\frac{-{{m}_{2}}{{v}_{2}}}{{{m}_{1}}}$

i.e. the gun and the bullet move in opposite directions, which is explained by the minus sign. 

2. Common velocity 

When two bodies collide with each other and if they combine after collision and move with the same velocity, that velocity is known as common velocity. 

The collision of two bodies and their common velocity are shown above. 

From the conservation of linear momentum m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂ 

After collision, if they move with the same velocity, v₁ = v₂ = v_c (common velocity) 

m₁u₁ + m₂u₂ = m₁v + m₂v 

or, m₁u₁ + m₂u₂ = v_c(m₁ + m₂)

$\therefore {{v}_{c}}=\frac{{{m}_{1}}{{u}_{1}}+{{m}_{2}}{{v}_{2}}}{{{m}_{1}}+{{m}_{2}}}$

Free body diagram:

The representation of bodies (mass) by points and various forces acting on them is called a free body diagram.

Types of forces to be discussed in free body diagram 

(i) Weight, w = mg 

(ii) Reaction, R 

(iii) Tension, T 

(iv) Upthrust, U 

(v) F_f is frictional force 

Equation of Force

Applied force – Opposing force = Resultant force 

i.e.    F_app – F_opp = ma

(a) Motion of lift 

(i) When the lift is moving upward

R – mg = ma 

$\therefore $ Effective weight, R = mg + ma (increases)

(ii) When the lift is moving downward 

mg – R = ma 

$\therefore $ Effective weight, R = mg – ma (decreases)

(iii) When the lift is moving downward with a = g 

Effective wt. mg – ma = m(g – a) = 0 (weightlessness/ free fall) 

(iv) Downward with a > g 

Effective wt. = mg – ma = – ve 

The body will strike the ceiling of the lift.

(b) Motion on frictionless pulley 

(i) For upward motion 

T – m₁g = m₁a

(ii) For downward motion 

m₂g – T = m₂a

Frictional force (F_f):

It is defined as the opposing force that comes in play between the contact surfaces of two bodies when one moves, slides, rolls or tends to do so. 

Causes of Friction 

1. Classical concept 

There are a large number of irregular projections on the surfaces of bodies, when one body is placed in contact with another and external force is applied, then these irregular projections begin to interlock and oppose the motion of the body. This is called frictional force. 

2. Molecular concept 

With increase in smoothness of the surfaces of two bodies in contact the area of contact also increases which increases the intermolecular force of attraction. Hence, the frictional force also increases. This is called the molecular concept of friction or cold-welding.

Types of Friction 

(i) Static Friction (F_FS)

It is defined as the frictional force which comes in play between the surfaces of two bodies, when one is in the state of rest over the surface of another and external force is applied. Its value is always equal to applied force.

i.e. F_FS = F_a 

(ii) Limiting friction (F_FL)

It is the maximum value of static frictional force or minimum value of force required just to move the object.

(iii) Kinetic friction (F_FK)

It is defined as the frictional force which comes in play between the surfaces of two bodies, when one is in the state of motion over the surface of another body. It is the force required to keep a body moving with uniform velocity. 

(iv) Rolling friction (F_FR)

It is defined as the frictional force which comes in play between the surfaces of two bodies, when one body rolls over the surface of another body. 

Note: 

Static friction > Kinetic friction > Rolling friction

Coefficient of Friction ($\mu $)

The frictional force is directly proportional to normal reaction, i.e.

F_f $\propto $ R 

F_f = $\mu $R 

$\mu $ = $\frac{{{F}_{f}}}{R}$

where, $\mu $ is proportionality constant known as coefficient of friction between the two surfaces. 

It is also defined as the ratio of frictional force to normal reaction. It has no unit.

Laws of friction:

The laws of friction are: 

(i) The friction force opposes the motion of the body and acts tangentially to the surface in contact.

(ii) The frictional force is directly proportional to the normal reaction 

i.e. F_f $\propto $ R

or, F_f = $\mu $R 

or, $\mu $ = $\frac{{{F}_{f}}}{R}$, where $\mu $ is the proportionality constant known as coefficient of friction between two surfaces.

(iii) The frictional force depends upon roughness or smoothness of the surface.

(iv) It is independent of the area of surface in contact. 

Experimental verification

 

Let us consider a wooden block placed on a horizontal surface. It is attached to a string which passes over a frictionless pulley carrying a scale pan at free end.

Small weights are added gradually on the pan till the wooden block just starts to slide. This shows the frictional force opposes the motion of the body and acts tangentially to the surface in contact verifying the first law.

When the block just starts to slide, the total weight added on the scale pan is equal to the limiting frictional force. The normal reaction (R) is equal to the weight of wooden black and the ratio $\frac{{{F}_{f}}}{R}$is calculated. The experiment is repeated by placing different masses on wooden blocks and forces of limiting friction are found each time. The rates are found to be constant. This verifies the second law.

The wooden block is replaced by blocks of different materials of the same weight. It is found that frictional force is different in each case. This verifies the third law.

If the wooden block is placed on its different sides with different areas, the same limiting frictional force is found which verifies the fourth law.

Q. What are the laws of friction? How are they verified? 

Angle of Friction ($\theta $):

It is defined as the angle made by the resultant of frictional force (F_f) and normal reaction (R) with normal reaction (R).

Let us consider an object of mass ‘m’ is placed on a horizontal surface. A force F_a is applied on the object so that the object just starts to move. The coefficient of friction between the object and the surface is $\mu $. The weight ‘mg’ acts vertically downward and normal reaction acts normally upward to the surface along OA. When the object just starts to move then applied force (F_a) = Limiting frictional force (F_f). Frictional force (F_f) acts in the direction opposite to the direction of motion along OC. Let us complete a parallelogram OABC. According to parallelogram law of vector addition, OB = F_R gives the resultant of frictional force (F_f) and normal reaction (R) as in figure above. By the definition, $\angle $AOB = $\theta $ is the angle of friction.

Now, tan$\theta $ = $\frac{AB}{OA}$ = $\frac{OC}{OA}$

$\therefore $ tan$\theta $ = $\frac{{{F}_{f}}}{R}$

$\therefore $ $\mu $ = $\frac{{{F}_{f}}}{R}$

$\therefore $$\mu $= tan$\theta $…….(a)

This shows that coefficient of friction is equal to tangent of angle of friction. 

Angle of Repose ($\alpha $):

It is defined as the angle made by an inclined plane with horizontal at which an object placed over it just starts to slide. 

Let us consider an object of mass ‘m’ just slides on an inclined plane which makes an angle α with the horizon. The weight ‘mg’ acts vertically downward, normal reaction ‘R’ acts normally outward to the surface. The frictional force ‘F_F‘ acts in the direction opposite to that of motion as in figure. Resolving the force ‘mg’ into its constituent, we get mgsin$\alpha $ and mgcos$\alpha $ as in figure. The component mgsin$\alpha $ is balanced by frictional force F_f,  

i.e. 

mgsin$\alpha $ = F_f …………. (i)  

And the component mg cos$\alpha $ is balanced by normal reaction R,

i.e. mg cos$\alpha $ = R ……….. (ii)

Dividing (i) by (ii),

$\frac{mgsin\alpha }{mg cos\alpha }$ = $\frac{{{F}_{f}}}{R}$

or, tan$\alpha $ = $\mu $ [ $\mu $ = F_F/R]

$\therefore $$\mu $= tan$\alpha $…………(b)

This shows that coefficient of friction is equal to tangent of angle of repose.

From equation (a), We have, 

$\mu $ = tan$\theta $ 

From equation (b), we have 

$\mu $ = tan$\alpha $

$\therefore $ tan$\alpha $ = tan$\theta $ 

$\therefore $$\alpha $ = $\theta $  

i.e. angle of repose is equal to angle of friction for a given pair of surfaces.

Q. Define angle of friction and angle of repose. Show that angle of friction is equal to angle of repose for a given pair of surfaces. 

Normal reaction in different cases: 

1. Horizontal surface 

R = mg

2. Inclined plane 

R = mg cos$\theta $

3. Lift moving upward 

R = mg + ma 

R – mg = ma 

4. Lift moving downward 

 

mg = R = ma

R = mg – ma

5. Case of pulling 

R = mg – Fsin$\theta $ 

mg = Fsin$\theta $ + R 

6. Case of pushing 

 

R = mg + Fsin$\theta $

NUMERICAL PROBLEMS

Dynamics

Q.1       A little red wagon with mass 7 kg moves in a straight line on a frictionless horizontal surface. It has an initial speed of 4 m/s and then is pushed 3 m in the direction of the initial velocity by a force of 10N. Calculate the wagon’s final speed and the acceleration produced by the force.

Ans: 4.96 m/sec, 1.43 m/sec²

Q.2       A cricket ball of mass 145 g is moving with a velocity of 14m/s and is being hit by a bat, so that the ball is turned back with a velocity of 22m/s. The force of blow acts on the ball for 0.015 sec. Find the average force exerted by the bat on the ball.

Ans: 348 N

Q.3       A vehicle having a mass of 500 kg moving with a speed of 10 ms^–1. Sand is dropped into it at the rate of 10 kg/min. What force is needed to keep the vehicle moving with a uniform peed?

Ans: F = 1.667 N

Q.4       The mass of gas emitted from the rear of toy rocket is initially 0.2 kgs^-1. If the speed of the gas relative to the rocket is 40 ms^-1, and the mass of rocket is 4 kg, what is the initial acceleration of the rocket?

Ans: 2 m/sec²

Q.5       A ball of mass 0.05 Kg strikes a smooth wall normally four times in 2 seconds with a velocity of 10ms^-1. Each time the ball rebounds with the same speed of 10ms^-1. Calculate the average force on the wall. Ans: 2 N

Q.6       A lift moves (i) up and (ii) down with an acceleration of 2ms^-2. In each case, calculate the reaction of the floor on a man of mass 50 kg standing in the lift.

Ans: 600 N, 400 N

Q.7       A 550N physics student stands on a bathroom scale in an elevator. As the elevator starts moving the scale reads 450N. Draw free body diagram of the problem and find the magnitude and direction of the acceleration of the elevator.

Ans: 1.8 m/sec²

Q.8       Two masses 7 kg and 12 kg are connected at the two ends of a light inextensible string that passes over a frictional pulley. Using free body diagram method, find the acceleration of masses and the tension in the string, when the masses are released.

Ans: 2.63 m/sec²; 88.42 N

Q.9       A 15 kg load of bricks hangs from one end of a rope that passes over a small, frictionless pulley. A 28 kg counterweight is suspended from the other end of the rope as shown in figure. The system is released from rest. Using free body diagram method, find the magnitude of upward acceleration of the load and the tension in the rope while the load is moving.

Ans: 3.02 m/sec² and 195.35 N

Q.10     A light rope is attached to a block with mass 4 kg that rests on a frictionless, horizontal surface. The horizontal rope passes over a frictionless pulley and a block with mass m is suspended from the other end. When the blocks are released, the tension in the rope is 10 N. Draw free body diagrams and calculate the acceleration of either block and the mass m of the hanging block.

Ans: 2.5 m/sec², 1.33 kg

Q.11     In a physics lab experiment, a 6 kg box is pushed across a flat table by a horizontal force F. If the box is moving at a constant speed of 0.35 m/s and the coefficient of kinetic friction is 0.12, what is the magnitude of F? If the box is speeding up with a constant acceleration of 0.18 m/s², what will be the magnitude of F?

Ans: (i) 7.2 N (ii) 8.28 N

Q.12     In a physics lab experiment, a 6kg box is pushed across a flat table by a horizontal force F. If the box is moving at a constant speed of 0.35m/s and the coefficient of kinetic friction is 0.12, find the magnitude of force F. What is the magnitude of force F if the box is moving with a constant acceleration 0.18 m/s²?

Ans: 7.2 N, 8.28 N

Q.13     A box of mass 15 kg placed on horizontal floor is pulled by a horizontal force. What will be the work done by the force if the coefficient of sliding friction between the box and the surface of the floor is 0.3 and body moved at unit distance.

Ans: 45 J

Q.14     What would be the acceleration of a block sliding down an inclined plane that makes an angle of 45^o with the horizontal if the coefficient of sliding friction between two surfaces in 0.3?

Ans: 4.95 m/sec

Q.15     An iron block of mass 10 kg rests on a wooden plane inclined at 30° to the horizontal. It is found that the least force parallel to the plane which causes the block to slide up is 100 N. Calculate the coefficient of friction between the two surfaces.

Ans: 0.577

Q.16     A chair of mass 10kg is sitting on a horizontal floor which is not frictionless. You push on the chair with a constant force of magnitude 30N which is directed at an angle of 30° below the horizontal and chair slides along the floor. Draw free-body diagram and calculate normal force that the floor exerts on the chair.

Ans: 115 N

Q.17     Suppose you try to move a crate by tying a rope around it and pulling on the rope at angle of 30° above the horizontal. What is the tension required to keep the crate moving with constant velocity? Assume weight of the crate ‘W’ = 500 N and coefficient of dynamic friction μ_k = 0.40.

Ans: 187.6 N

**********

Q.18 A rubber ball of mass 200gm falls from a height of 5m and rebounds to a height of 4m. Find the impulse and the average force between the ball and the ground if the time during which they are in contact was 0.2 sec

Ans: 3.8 kgms^-1 , 18.9N

Q.19 How large must force ‘F’ be to give to 500gm block acceleration of 20 cm/s2 placed on horizontal table? [The coefficient of friction between the block and the table is 0.2]

Ans: 1.1 N

Q.20 A 4 kg object moving with a velocity of 4m/s collides with 12 kg object moving with a velocity of 2m/salong the same line. If the two objects coalesce after collision, calculate their common velocity when they are initially moving (a) in the same direction (b) in the opposite direction.

Ans: 3.3m/s, 2 m/s

Q.21 A block slides down a plane inclined at 45^o to the horizontal. Find the acceleration of the block (a) if the plane is frictionless (b) If the coefficient of kinetic friction is 0.3.

Ans:7.07m/s², 4.95m/s²

Q.22 Find the acceleration of the following system and the tension in the cord. Assume the surface and pulley are frictionless.

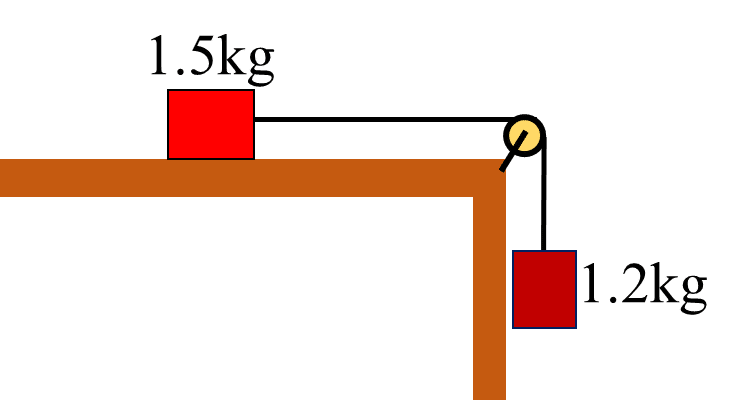
Ans: 4.44 m/s², 6.67 N

Q.23 Find the acceleration of the following system and the tension in the cord. Assume the surface and pulley are frictionless.

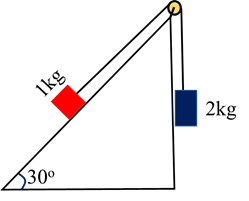
Ans: 5 m/s², 10 N

Q.24 Two masses connected by a string which passes over a small frictionless pulley rest on frictionless plane as shown in the diagram. (i) which way will the system move? What is the acceleration of the system? (iii) What is the tension in the string?

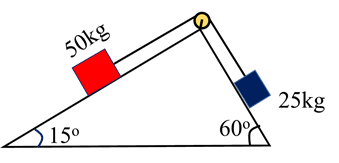
Ans: 25kg slides down, 1.16 m/s², 187.46N

**********

Also Read: Kinematics Notes Class 11