Thermoelectric effect / Seebeck effect:
The phenomenon of production of electricity by keeping junctions of two different metals at different temperatures is known as thermoelectric effect.
The emf is known as thermoelectric emf and the current is thermoelectric current.
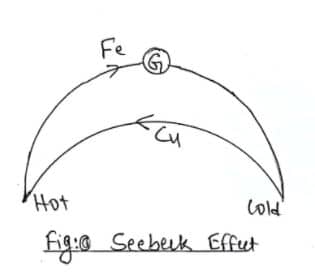
Thermocouple:
The loop of two different metals which can produce thermoelectricity when two different junctions are placed at different temperatures is known as thermocouple.
Variation of thermoelectric emf with temperature:
Fig: Copper-Iron thermocouple
To study the variation of thermoelectric emf with temperature, a Cu- Fe thermocouple provided with a sensitive galvanometer is used. Let X and Y be the two junctions of thermocouple. The junction X is placed inside hot oil bath that is at higher temperature and junction Y is place in melting of ice to maintain a constant temperature. On doing so, an emf (E) will be setup and the galvanometer shows deflection.
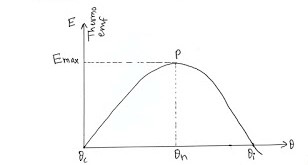
On increasing the temperature of hot junction, it is found that the thermoelectric emf also increases and becomes maximum for a particular value of temperature, known as neutral temperature (${{\theta }_{n}}$). It depends upon the nature of the material only.
If temperature of hot junction is further increased, the thermoelectric emf starts to decrease and becomes zero for particular value of temperature which is known as temperature of inversion (${{\theta }_{i}}$). It depends upon nature of the thermocouple and the temperature of cold junction (${{\theta }_{c}}$). If temperature of hot junction is increased beyond the temperature of inversion, the direction of thermoelectric emf gets inverted i.e. current starts to flow in the opposite direction.
If a graph is plotted between thermoelectric emf and temperature, a parabola will be obtained as shown in figure below.
Now we can write,
E = a$\theta $ + b$\theta $2 where ‘a’ and ‘b’ are constants.
As the nature of the curve is parabolic then we can write,
${{\theta }_{n}}$ – ${{\theta }_{c}}$= ${{\theta }_{i}}$ – ${{\theta }_{n}}$
Or, 2${{\theta }_{n}}$ = ${{\theta }_{i}}$ + ${{\theta }_{c}}$
$\therefore $ ${{\theta }_{n}}$ = $\frac{{{\theta }_{i}}+{{\theta }_{c}}}{2}$
So the neutral temperature lies exactly between inversion temperature and temperature of cold junction.
Relation between thermoelectric constants a, b, ${{\theta }_{c}}$ and ${{\theta }_{i}}$:
Let us consider a thermocouple whose cold junction is kept at 0°C and the temperature of hot junction be ‘$\theta $’.
Then we have thermoelectric emf is
E = a$\theta $ + b$\theta $2 ………… (i)
Differentiating above equation with respect to temperature ‘$\theta $’, we get
$\frac{dE}{d\theta }$= $\frac{d}{d\theta }$ (a$\theta $+b$\theta $2)
Or, $\frac{dE}{d\theta }$= a +2b$\theta $
At $\theta $ =${{\theta }_{n}}$, E is maxm (constant) $\therefore $$\frac{dE}{d\theta }$= 0
Then above equation becomes,
0 = a + 2b${{\theta }_{n}}$
$\therefore $ ${{\theta }_{n}}$ = $\frac{-a}{2b}$ ……….. (ii)
Again, at $\theta $ = ${{\theta }_{i}}$, E = 0
Then equation (i) becomes,
0 = a${{\theta }_{i}}$ + b${{\theta }_{i}}$2
Or, ${{\theta }_{i}}$(a+ b${{\theta }_{i}}$) = 0
As ${{\theta }_{i}}$ ≠ 0 ∴(a+ b${{\theta }_{i}}$) = 0
$\therefore $${{\theta }_{i}}$ = $\frac{-a}{b}$………. (iii)
Hence, ${{\theta }_{n}}$ = $\frac{-a}{2b}$and ${{\theta }_{i}}$ = $\frac{-a}{b}$are the relations between thermoelectric constants a, b, ${{\theta }_{n}}$ and ${{\theta }_{i}}$.
Thermoelectric series:
The arrangement of different metals in the form of series from which any two metals can be used for used to form a thermocouple is known as thermoelectric series.
Sb, As, Fe, Cd, Zn, Ag, Au, Mo, Sn, Pb, Hg, Mn, Cu, Pt, Co, Ni, Bi
The first member of thermoelectric series is antimony (Sb) and last member is bismuth (Bi). More the separation between two metals in the series, more is the value of thermoelectric current.
Thermoelectric Power:
The rate of chance of thermo emf (E) with respect to temperature ($\theta $) is called thermoelectric power. It is denoted by ‘P’ and given by P = $\frac{dE}{d\theta }$.
Peltier effect:
When an electric current is passed through a thermocouple, heat is either evolved or absorbed at the junction, depending upon the direction of flow of current. This effect is called Peltier effect. If the direction of current is reversed, the evolution or absorption of heat at the junctions are interchanged.
This effect is the inverse process of Seebeck effect.
Q. The thermo-emf (E) and the temperature of hot junction $\theta $ satisfies the relation E = a$\theta $ + b${{\theta }^{2}}$ where a= 4.1×10–5 V (oC)–1 and b = – 4.1×10–8 V (oC)–2 . If the cold junction temperature is 0oC, find the neutral temperature.
Solution
Here,E = a$\theta $ + b${{\theta }^{2}}$
a = 4.1×10–5 V (oC)–1
b = – 4.1×10–5 V (oC)–2
Neutral temperature, ${{\theta }_{n}}$= ?
From the relations between thermoelectric constants, we have
${{\theta }_{n}}$= $\frac{-a}{2b}$
Or, ${{\theta }_{n}}$= $\frac{-\text{ }4.1\times {{10}^{5}}}{-2\times 4.1\times {{10}^{8}}}$= 500 oC
Q. A thermocouple has 540 oC as its temperature of inversion when its cold junction is at 0 oC. Find the temperature of inversion, if cold junction is at 30 oC.
Solution
Here,
Case-1:
Temperature of inversion, ${{\theta }_{i}}$= 540 oC when temperature cold junction, ${{\theta }_{c}}$ = 0 oC
We have,
${{\theta }_{n}}$ = $\frac{{{\theta }_{i}}+\theta {}_{c}}{2}$ = $\frac{540+0}{2}$= 270 oC
Case-2:
Temperature of inversion, ${{\theta }_{i}}$= ?, when temperature cold junction, ${{\theta }_{c}}$ = 30 oC
(The neutral temperature remains same for given thermocouple)
Again, ${{\theta }_{n}}$ = $\frac{{{\theta }_{i}}+\theta {}_{c}}{2}$
Or, 270 = $\frac{{{\theta }_{i}}+30}{2}$
Or, ${{\theta }_{i}}$= 270×2–30 = 510 oC
Also Read: Heating Effect of Current Class 12
Your style is very unique compared to other people I’ve read stuff from.
Thanks for posting when you have the opportunity,
Guess I will just bookmark this blog.